In the previous literature, 1.5-dimensional spectrum can be used to detect the secondary phase coupling, that is to say, frequency coupling and phase coupling should be met simultaneously in the detected signals. However, in the actual vibration signals, the frequency components that meet the frequency coupling generally do not meet the phase coupling. Therefore, the author proposes a 1.5-dimensional spectrum, which can be used to detect only the secondary frequency coupling from the vibration signal, which is helpful to the detection of the actual vibration signal.
Set the vibration signal as follows:

Where: AI is the amplitude constant; ω I is the angular frequency; φ I is the independent random variable uniformly distributed on [0,2 π).
The Fourier transform of X (T) is as follows:

Where: δ (·) – pulse function.
According to whether the third-order cumulants are conjugate or not, there are eight definitions for the third-order cumulants of complex harmonic signals. The author then takes one of them to prove that the components generated by secondary frequency coupling can be detected.
The form of one-dimensional diagonal slice of the third-order cumulant of the complex harmonic signal is as follows:
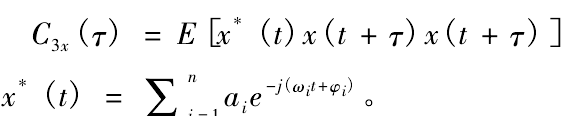
According to the definition, the one-dimensional diagonal slice spectrum of the third-order cumulant can be obtained as follows:


Substituting x * (ω) and X (ω) into the formula, we can get the following results:

According to the properties of impulse function, when ω K – ω = 0, that is, ω = ω K, the formula is not 0, and then the formula becomes:

According to the properties of the pulse function, only when ω K – ω p – ω q = 0, that is, ω k = ω P + ω Q, the formula is not 0, and there is amplitude on the spectrum, so the 1.5-dimensional spectrum can detect the secondary frequency coupling.
In this case, no matter what the value of phase φ K – φ p – φ q is, the amplitude of secondary frequency coupling will not be affected. Therefore, the application of 1.5-dimensional spectrum only needs to meet the frequency coupling, not the phase coupling, which is of great significance for the application of 1.5-dimensional spectrum in the actual vibration signal.
