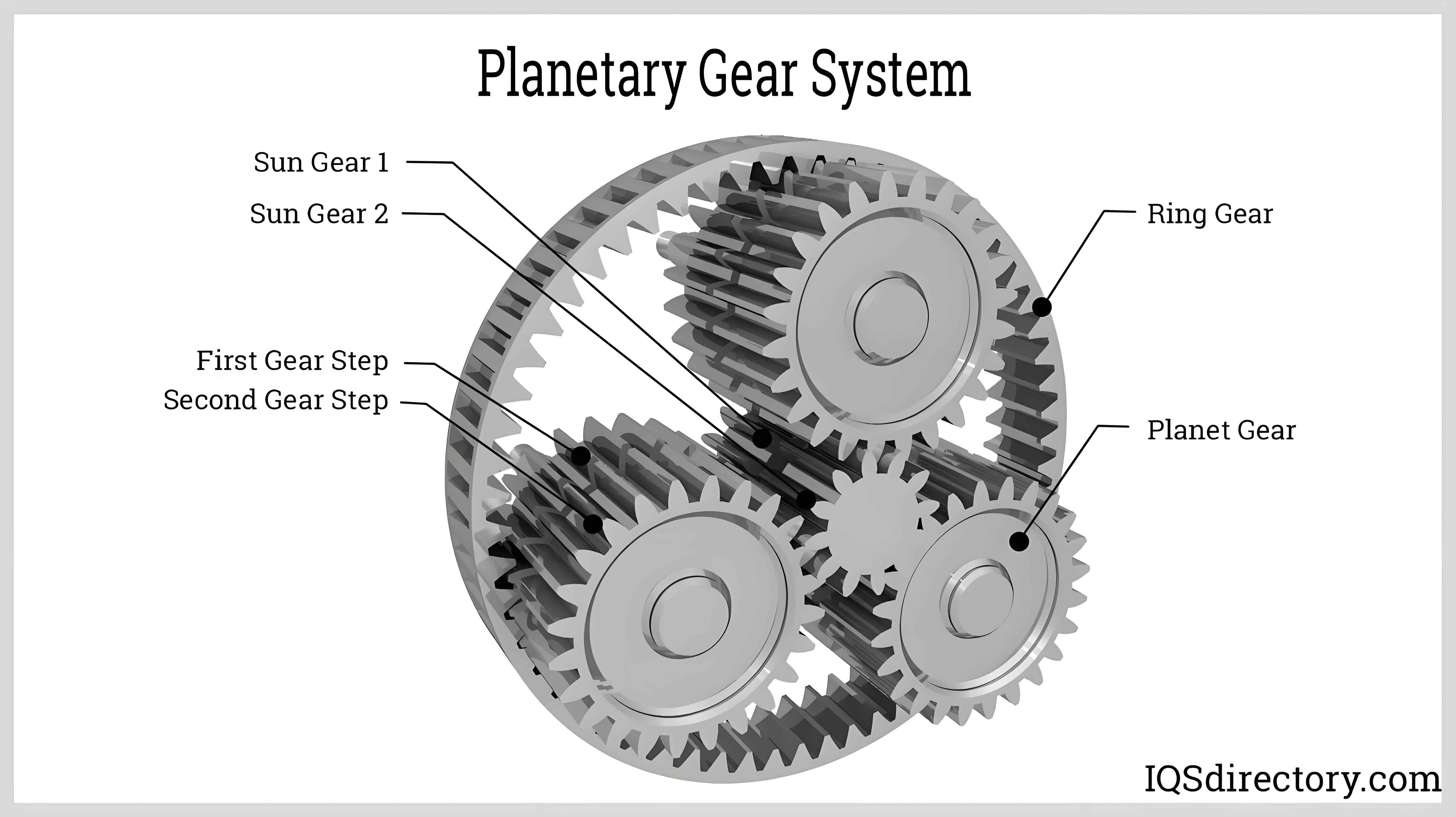
In the field of mechanical engineering, planetary gear systems have garnered significant attention due to their compact design, high torque density, and efficient power transmission. Among various configurations, the linear conjugate planetary gear transmission with small tooth difference stands out for its potential to enhance performance in reducers and other applications. This study focuses on developing a comprehensive mathematical model, conducting dynamic simulations, and performing experimental validations to analyze the meshing forces and vibration characteristics of such systems. The primary goal is to provide a theoretical foundation and practical insights for optimizing planetary gear designs, with particular emphasis on the unique attributes of linear conjugate tooth profiles. Throughout this research, the behavior of planet gears under different operational conditions is thoroughly investigated to ensure reliability and efficiency.
The mathematical modeling of the linear conjugate planetary gear system begins with the derivation of the external gear tooth profile. Consider a coordinate system \( S_1: O_1 – x_1 y_1 \) for the external gear, as illustrated in the referenced figure. The tooth profile consists of linear segments, and its mathematical representation can be expressed as follows. Let \( b \) represent the intercept of the linear profile, and \( k \) denote its slope. The coordinates \( x_a \), \( x_b \), and \( x_c \) correspond to points a, b, and c on the profile, respectively. These are defined by the equations:
$$ b = r_1 \cos \theta + r_1 \sin \theta \cot \beta $$
$$ k = -\cot \beta $$
$$ x_a = \text{value based on geometric constraints} $$
Thus, the mathematical model for the external gear tooth profile is given by:
$$ \mathbf{R}_1 = \begin{bmatrix} x_{1p} \\ y_{1p} \end{bmatrix} = f(s, Z, R, \beta) $$
where \( s \) is a parameter along the tooth profile, \( Z \) represents the number of teeth, \( R \) is the reference radius, and \( \beta \) is the pressure angle. This formulation allows for precise control over the gear geometry, which is crucial for minimizing vibrations and ensuring smooth operation in planetary gear arrangements.
For the internal gear tooth profile, the principles of gear meshing theory are applied. The internal profile is derived as the envelope of the external gear’s tooth profile during the meshing process. The transformation from the external gear coordinate system \( S_1 \) to the internal gear system \( S_2 \) is achieved through a coordinate transformation matrix \( \mathbf{M}_{21} \), which accounts for the relative rotation and displacement between the gears. The internal gear tooth profile \( \mathbf{R}_2 \) is described by:
$$ \mathbf{R}_2 = \mathbf{M}_{21} \cdot \mathbf{R}_1 $$
where the transformation matrix \( \mathbf{M}_{21} \) is defined as:
$$ \mathbf{M}_{21} = \begin{bmatrix} \cos(\phi_1 – \phi_2) & -\sin(\phi_1 – \phi_2) & r_2 \sin \phi_1 – r_1 \sin \phi_2 \\ \sin(\phi_1 – \phi_2) & \cos(\phi_1 – \phi_2) & r_2 \cos \phi_1 – r_1 \cos \phi_2 \\ 0 & 0 & 1 \end{bmatrix} $$
Here, \( \phi_1 \) and \( \phi_2 \) are the rotation angles of the external and internal gears, respectively, and \( r_1 \), \( r_2 \) are their pitch radii. The necessary condition for the existence of the envelope curve is given by the equation of meshing, which ensures continuous contact between the gears. This condition involves the relative velocity vector \( \mathbf{v}_{12} \) and is expressed as:
$$ \mathbf{v}_{12} \cdot \mathbf{n} = 0 $$
where \( \mathbf{n} \) is the normal vector to the tooth profile. Solving these equations yields the relationship between the parameters \( \phi_1 \) and \( x \), leading to a complete mathematical model for the internal gear. This model is essential for simulating the dynamic behavior of planet gears in the system, as it accurately captures the interaction between meshing components.
Dynamic simulation of the planetary gear system involves analyzing the meshing forces and vibration characteristics under various operating conditions. The simulations were conducted for multiple scenarios to assess the impact of input speed and load torque on system performance. For instance, with a constant load torque of 80 N·m, input speeds of 600 rpm, 1,400 rpm, and 2,200 rpm were considered, denoted as Condition 1, Condition 2, and Condition 3, respectively. Similarly, with a fixed input speed of 1,400 rpm, load torques of 40 N·m, 80 N·m, and 120 N·m were evaluated as Condition 4, Condition 2, and Condition 5. The simulation time was set to 1 second with a step size of 2.5 × 10^{-3} seconds to ensure accuracy.
The dynamic meshing force simulations revealed that the forces fluctuate around a mean value due to factors such as eccentric forces, unbalanced inertial forces, time-varying mesh stiffness, and tooth deformations. Under Condition 1 (600 rpm, 80 N·m), the root mean square (RMS) value of the meshing force was approximately 1,219.86 N, with a theoretical calculation of 1,303.69 N, resulting in an error of 6.87%. As the input speed increased to 1,400 rpm and 2,200 rpm under the same load, the RMS values decreased slightly to 1,214.07 N and 1,208.66 N, respectively, indicating a positive correlation between speed and force fluctuations. This behavior highlights the importance of considering dynamic effects in planetary gear designs to prevent premature fatigue and ensure longevity.
When varying the load torque at a constant input speed of 1,400 rpm, the meshing forces showed a significant increase. For Condition 4 (40 N·m), the RMS value was 606.18 N, while for Condition 5 (120 N·m), it rose to 1,849.17 N. The theoretical values for these conditions were 651.85 N and 1,951.64 N, with errors of 7.01% and 5.41%, respectively. These results are summarized in the table below, which provides a comprehensive overview of the dynamic meshing force simulations under typical operating conditions. The table illustrates how planetary gears respond to changes in operational parameters, emphasizing the need for robust design practices.
| Condition | Max Force (N) | RMS Force (N) |
|---|---|---|
| 600 rpm, 80 N·m | 1,453.54 | 1,219.86 |
| 1,400 rpm, 80 N·m | 1,492.75 | 1,214.07 |
| 2,200 rpm, 80 N·m | 1,628.77 | 1,208.66 |
| 1,400 rpm, 40 N·m | 912.66 | 606.18 |
| 1,400 rpm, 120 N·m | 2,139.88 | 1,849.17 |
Vibration characteristics were also simulated to evaluate the system’s dynamic response. The analysis focused on nodes 310 and 580 of the fixed internal gear, measuring vibration accelerations in the X (axial), Y (circumferential), and Z (radial) directions. Under Condition 2 (1,400 rpm, 80 N·m), the vibration acceleration peaked in the Z-direction due to instantaneous meshing impacts when the gears engaged. Specifically, the planet gears exhibited five distinct peaks within 0.1 seconds, corresponding to the meshing frequency and the gear tooth difference of 2. This pattern underscores the cyclic nature of vibrations in planetary gear systems, which can lead to noise and wear if not properly managed.
As input speed increased from 600 rpm to 2,200 rpm under a constant load of 80 N·m, the vibration acceleration RMS values rose from 0.296 m/s² to 1.693 m/s², demonstrating a positive correlation between speed and vibration intensity. Similarly, when load torque increased from 40 N·m to 120 N·m at 1,400 rpm, the vibration acceleration increased from 0.742 m/s² to 0.977 m/s². These trends are critical for designing planetary gear systems that operate under variable conditions, as excessive vibrations can compromise performance and reliability. The following table compares the simulated and experimental vibration acceleration RMS values, highlighting the consistency between theory and practice.
| Condition | Simulated RMS (m/s²) | Experimental RMS (m/s²) | Error (%) |
|---|---|---|---|
| 600 rpm, 80 N·m | 0.296 | 0.269 | 9.12 |
| 1,400 rpm, 80 N·m | 0.879 | 0.818 | 6.94 |
| 2,200 rpm, 80 N·m | 1.693 | 1.537 | 9.21 |
| 1,400 rpm, 40 N·m | 0.742 | 0.701 | 5.53 |
| 1,400 rpm, 120 N·m | 0.977 | 0.929 | 6.96 |
Experimental research was conducted to validate the simulation results, using a dynamic signal testing system with IEPE piezoelectric acceleration sensors. The test setup involved attaching sensors to the external surface of the fixed internal gear to capture vibration signals under the same operational conditions as the simulations. The time-domain responses showed that vibration acceleration increased with both input speed and load torque, corroborating the simulation findings. For example, under Condition 1 (600 rpm, 80 N·m), the experimental RMS value was 0.269 m/s², while under Condition 3 (2,200 rpm, 80 N·m), it reached 1.537 m/s². This experimental data confirms the dynamic behavior of planet gears and their sensitivity to operational parameters.
Frequency domain analysis of the vibration signals was performed using Fast Fourier Transform (FFT) to identify dominant frequency components. The spectra revealed peaks at frequencies corresponding to the input shaft rotational frequency, meshing frequency, and its harmonics. For instance, at 600 rpm, the peak frequency was 765.25 Hz, with sidebands at ±60 Hz, while at 1,400 rpm, the peak averaged 1,718.63 Hz with sidebands at ±80 Hz. The theoretical meshing frequencies for these conditions were 720 Hz, 1,680 Hz, and 2,640 Hz, with errors of 6.28%, 2.26%, and 2.19%, respectively. These results indicate that the vibration characteristics are closely tied to the meshing dynamics of planet gears and that no resonance occurred, as the frequencies did not overlap with the system’s natural modes.
The mathematical models and simulation approaches developed in this study provide a robust framework for analyzing linear conjugate planetary gear systems. The external gear tooth profile is derived using parametric equations that account for the linear segments and geometric constraints. For example, the coordinate \( x_{1p} \) can be expressed as a function of the profile parameter \( s \), and the slope \( k \) is determined by the pressure angle \( \beta \). The internal gear profile is then obtained through coordinate transformations and the equation of meshing, ensuring accurate representation of the gear pair interaction. These models are fundamental for predicting the performance of planet gears under various loads and speeds.
In the dynamic simulations, the meshing forces are calculated using the derived tooth profiles and the principles of dynamics. The force variations are influenced by factors such as the time-varying mesh stiffness \( k_m(t) \), which can be modeled as a periodic function. For instance, the mesh stiffness for a planetary gear system can be approximated as:
$$ k_m(t) = k_0 + \sum_{n=1}^{\infty} k_n \cos(n \omega_m t + \phi_n) $$
where \( k_0 \) is the average stiffness, \( k_n \) are the harmonic components, \( \omega_m \) is the meshing frequency, and \( \phi_n \) are phase angles. This formulation helps in understanding the fluctuations in meshing forces and their impact on vibration. Additionally, the dynamic equations of motion for the planetary gear system can be written as:
$$ \mathbf{M} \ddot{\mathbf{x}} + \mathbf{C} \dot{\mathbf{x}} + \mathbf{K} \mathbf{x} = \mathbf{F}(t) $$
where \( \mathbf{M} \), \( \mathbf{C} \), and \( \mathbf{K} \) are the mass, damping, and stiffness matrices, respectively, \( \mathbf{x} \) is the displacement vector, and \( \mathbf{F}(t) \) is the external force vector. Solving these equations numerically allows for the simulation of vibration responses and meshing forces under different conditions.
The experimental setup involved a DH5922 dynamic signal testing system, which recorded vibration signals at a sampling rate of 256 kHz per channel. The sensors were calibrated to ensure accuracy, and the data was processed using specialized software to obtain time-domain and frequency-domain analyses. The close agreement between simulated and experimental results, with errors generally below 10%, validates the mathematical models and simulation techniques. This consistency is crucial for advancing the application of linear conjugate tooth profiles in planetary gear systems, as it demonstrates the reliability of predictive tools in real-world scenarios.
In conclusion, this research comprehensively addresses the simulation and experimental analysis of linear conjugate planetary gear transmission with small tooth difference. The mathematical models accurately describe the tooth profiles and meshing behavior, while dynamic simulations reveal the effects of input speed and load torque on meshing forces and vibrations. Experimental results confirm these findings, showing that vibration acceleration increases with both speed and load. The insights gained from this study provide a solid foundation for optimizing planetary gear designs, particularly in applications requiring high precision and durability. Future work could focus on extending these models to include thermal effects or exploring alternative tooth profiles for enhanced performance. Overall, the integration of theoretical and experimental approaches ensures that planetary gear systems can be designed and operated with greater confidence and efficiency.
