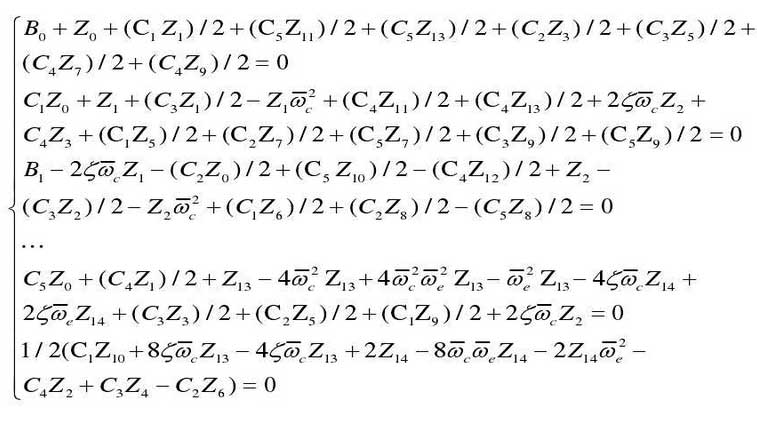Considering the harmonic balance between the left and right sides of the formula, the angular acceleration term on the right side of the formula is expanded by Fourier series, and the harmonics of ω C and 2 ω C are substituted into the formula
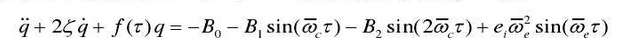
Where B1 and B2 are the coefficients of Fourier series expansion of angular acceleration term respectively.
Based on the above analysis process of harmonic components of the vibration response of the reducer variable speed integrated gear, it is assumed that the basic form of the steady-state response of the gear is as follows:
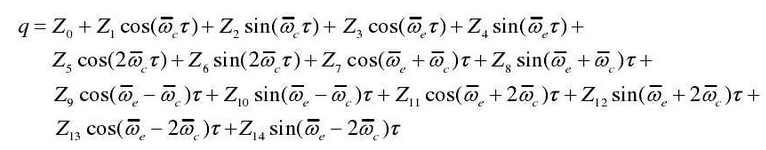
Although sinusoidal harmonics have little effect on the overall amplitude, the introduction of sinusoidal harmonics can introduce damping into the amplitude, so resonance will not occur many times. In the numerical calculation, if the damping is removed, resonance can indeed occur. The numerical solution can correspond to the analytical method at low frequency, but it can not be corresponding at high frequency.
According to the harmonic balance method, a set of 15 unknowns (Z0, Z1 Z14) is shown in the formula. By solving the equations, the steady-state response of the reducer variable speed integrated gear can be obtained, and the steady-state response obtained by solving the linear equation group is further analyzed.