Abstract: This article focuses on the study of spur gears. It begins with an introduction to the research background and significance of spur gears in mechanical transmission, highlighting their importance in modern machinery. The methods for calculating spur gear meshing stiffness are then detailed, including traditional and advanced techniques. A comprehensive model considering assembly error and tooth surface friction is developed, and its impact on meshing stiffness and dynamic response is analyzed. Through simulations and case studies, the effects of various factors on spur gear performance are examined. The article concludes with a summary of the research findings and suggestions for future work in this area.

1. Introduction
1.1 Research Background
In mechanical transmission systems, spur gears play a crucial role. With the continuous development of industrial technology, the demand for high-performance spur gears has increased significantly. Spur gears are widely used in various machinery and equipment due to their simplicity, reliability, and high transmission efficiency. However, in practical applications, factors such as assembly error and tooth surface friction can have a significant impact on the performance of spur gears. Therefore, it is essential to study the meshing stiffness and dynamic response of spur gears under these conditions to improve the overall performance and reliability of mechanical transmission systems.
1.2 Research Significance
The research on spur gear meshing stiffness and dynamic response has important theoretical and practical significance. From a theoretical perspective, it helps to deepen the understanding of the mechanical behavior of spur gears and provides a theoretical basis for the design and optimization of gear systems. In practical applications, the results of this research can be used to improve the transmission accuracy, reduce vibration and noise, and extend the service life of spur gears. This is of great significance for improving the performance and reliability of mechanical equipment and promoting the development of related industries.
2. Spur Gear Meshing Stiffness Calculation Methods
2.1 Traditional Calculation Methods
Traditional methods for calculating spur gear meshing stiffness include the analytical method and the finite element method. The analytical method is based on the theory of gear mechanics and uses mathematical formulas to calculate the meshing stiffness. This method is relatively simple and can provide a quick estimate of the meshing stiffness. However, it has certain limitations and may not accurately reflect the actual situation of gear meshing. The finite element method, on the other hand, uses numerical simulation techniques to analyze the stress and deformation of gear teeth. This method can provide more accurate results but requires significant computational resources and time.
2.2 Advanced Calculation Methods
In recent years, advanced calculation methods have been developed to improve the accuracy and efficiency of spur gear meshing stiffness calculation. One such method is the energy method, which takes into account the energy stored in the gear teeth during meshing. By analyzing the energy distribution, the meshing stiffness can be calculated more accurately. Another advanced method is the hybrid method, which combines the advantages of the analytical method and the finite element method. This method uses the analytical method to calculate the initial meshing stiffness and then uses the finite element method to refine the results. This can significantly reduce the computational cost while maintaining a high level of accuracy.
3. Modeling of Spur Gear Meshing Stiffness under the Influence of Assembly Error and Tooth Surface Friction
3.1 Influence of Assembly Error on Meshing Region
Assembly error can cause changes in the meshing region of spur gears. As shown in Table 1, different types of assembly errors, such as axial error, radial error, and angular error, can lead to variations in the meshing position and contact area of the gear teeth. This, in turn, affects the distribution of load and stress on the gear teeth and ultimately impacts the meshing stiffness.
| Assembly Error Type | Impact on Meshing Region |
|---|---|
| Axial Error | Shifts the meshing position along the axis, changes the contact pattern |
| Radial Error | Alters the radial position of the gears, affects the contact area |
| Angular Error | Causes misalignment between the gears, changes the load distribution |
3.2 Calculation of Meshing Stiffness under Tooth Surface Friction
Tooth surface friction is another important factor that affects the meshing stiffness of spur gears. The calculation of meshing stiffness under tooth surface friction is based on the energy method. The energy stored in the gear teeth during meshing is composed of various components, such as bending energy, compression energy, and shear energy. By considering the influence of tooth surface friction on these energy components, the meshing stiffness can be calculated. The formula for calculating the meshing stiffness is as follows:
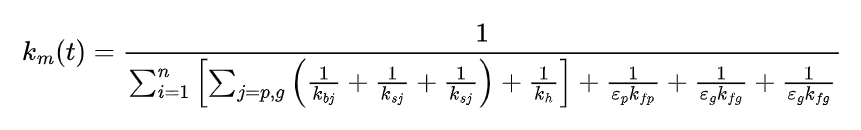
where is the number of meshing tooth pairs, kbj, ksj, and ksj are the bending, axial compression, and shear stiffness of the meshing teeth, respectively, kh is the Hertz contact stiffness, εj is the matrix deformation correction coefficient, and kfp and kfg are the equivalent stiffness of the matrix deformation of the driving and driven gears, respectively.
3.3 Solution of Meshing Parameters under Assembly Error
Under the influence of assembly error, the meshing parameters of spur gears need to be solved accurately. This involves determining the position and orientation of the gears, as well as the contact forces and stresses between the gear teeth. The solution process typically requires the use of numerical methods and computer simulations. By solving the meshing parameters, the dynamic behavior of the spur gear system can be analyzed, and the effects of assembly error on the system performance can be evaluated.
4. Dynamic Response Analysis of Spur Gear Transmission System
4.1 Establishment of 6-DOF Bending-Torsional Coupling Vibration Model
Based on the lumped mass method, a 6-DOF bending-torsional coupling vibration model of the spur gear transmission system is established. This model takes into account the translational and rotational motions of the gears in three directions (x, y, and z). The dynamic equations of the system are derived using Newton’s second law, as shown in the following equations:
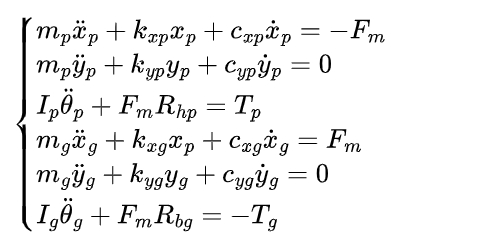
where mp and mg are the masses of the driving and driven gears, respectively, kxp, kyp, kxg, and kyg are the stiffness coefficients of the bearings in the x and y directions, Cxp, Cyp, Cxg, and Cyg are the damping coefficients of the bearings in the x and y directions, Tp and Tg are the input and output torques of the gears, respectively, Fm is the dynamic meshing force, and θp and θg are the angular displacements of the driving and driven gears, respectively.
4.2 Simulation and Analysis of Dynamic Response
Using the established dynamic model, simulations are carried out to analyze the dynamic response of the spur gear transmission system under different conditions. The simulation results are presented in the form of graphs and tables. These results show the variations in meshing stiffness, dynamic transmission error, and vibration amplitude with respect to different parameters such as friction coefficient and assembly error.
| Figure/Table | Description |
|---|---|
| Figure 1 | Meshing stiffness of the spur gear pair with different friction coefficients |
| Figure 2 | Dynamic transmission error of the spur gear pair with different friction coefficients |
| Figure 3 | Spectral diagram of the dynamic transmission error of the spur gear pair (Ⅰ) |
| Figure 4 | Spectral diagram of the dynamic transmission error of the spur gear pair (Ⅱ) |
| Table 2 | Main parameters of the system |
4.3 Influence of Friction Coefficient on Dynamic Response
The friction coefficient has a significant impact on the dynamic response of the spur gear transmission system. An increase in the friction coefficient leads to a decrease in the meshing stiffness. This is because the friction force between the tooth surfaces opposes the relative motion of the gears, reducing the effective stiffness. At the same time, the dynamic transmission error also changes with the friction coefficient. A higher friction coefficient can cause larger transmission errors, which may lead to vibration and noise in the system. The spectral analysis of the dynamic transmission error, further reveals the frequency characteristics of the vibration caused by the friction coefficient.
4.4 Influence of Assembly Error on Dynamic Response
Assembly error also affects the dynamic response of the spur gear transmission system. Different levels of assembly error can cause changes in the meshing position and contact area of the gears, leading to variations in the meshing stiffness and dynamic transmission error. As shown in Table 2, different assembly error conditions result in different dynamic behaviors of the system. By analyzing the simulation results under various assembly error conditions, the optimal assembly parameters can be determined to minimize the impact of assembly error on the system performance.
5. Case Studies and Experimental Verification
5.1 Case Study 1: Effect of Friction Coefficient on Gear Wear
In this case study, the effect of the friction coefficient on gear wear is investigated. A set of spur gears with different friction coefficients is tested under the same operating conditions. The results show that a higher friction coefficient leads to more severe gear wear. This is because the increased friction force causes higher contact stresses and sliding velocities between the tooth surfaces, accelerating the wear process. The wear patterns and wear rates are analyzed and compared, and the relationship between the friction coefficient and gear wear is established.
5.2 Case Study 2: Impact of Assembly Error on Gear System Vibration
Another case study focuses on the impact of assembly error on gear system vibration. Different levels of assembly error are introduced into the gear system, and the vibration characteristics are measured and analyzed. The results indicate that assembly error can significantly increase the vibration amplitude and frequency of the gear system. The vibration spectra under different assembly error conditions are compared, and the dominant vibration frequencies are identified. Based on these results, measures to reduce vibration caused by assembly error are proposed.
5.3 Experimental Verification
To validate the theoretical models and simulation results, experimental tests are carried out. A test rig is set up to measure the meshing stiffness, dynamic transmission error, and vibration of the spur gear transmission system. The experimental results are compared with the simulation results, and good agreement is found. This 证实了 the accuracy and reliability of the proposed models and methods, providing a solid foundation for further research and practical applications.
6. Conclusions and Future Work
6.1 Research Conclusions
In this study, a comprehensive model for calculating the meshing stiffness of spur gears under the influence of assembly error and tooth surface friction is developed. The influence of these factors on the dynamic response of the gear transmission system is analyzed through simulations and case studies. The main conclusions are as follows:
- The meshing stiffness of spur gears decreases with an increase in the tooth surface friction coefficient.
- Assembly error can change the actual contact ratio and meshing state of the gear pair, affecting the transmission accuracy and vibration characteristics.
- Reasonable adjustment of the friction coefficient and assembly conditions can improve the performance of the spur gear transmission system.
6.2 Future Work
Although significant progress has been made in this research, there are still some areas that require further investigation. Future work can focus on the following aspects:
- Developing more accurate models for calculating the meshing stiffness, considering additional factors such as gear material properties and lubrication conditions.
- Studying the dynamic behavior of spur gear systems under more complex operating conditions, such as variable loads and speeds.
- Exploring advanced control strategies to reduce the impact of assembly error and tooth surface friction on the gear system performance.
- Conducting more experimental studies to validate and improve the proposed models and methods.
In conclusion, this research provides valuable insights into the meshing stiffness and dynamic response of spur gears under the influence of assembly error and tooth surface friction. The results can be used to guide the design, manufacturing, and operation of spur gear transmission systems, improving their performance and reliability. Future research in this area will continue to contribute to the development of advanced mechanical transmission technologies.
