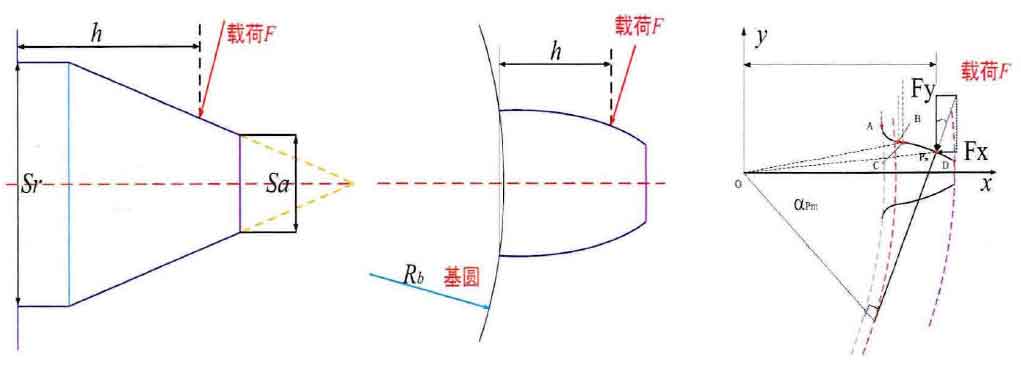
(b) Variable section cantilever beam on the gear base circle
(c) Detail involute profile tooth model
The analytic method of potential energy is mainly based on the elastic mechanics theory and the elastic deformation energy under the action of the load on the structure. As shown in figure, in turn, made in tooth stiffness analytic method used to calculate the evolution model, which is suitable for early ishikawa diagram (a) method to calculate the approximate tooth shape, using trapezoidal and rectangular cantilever beam structure composed of tooth shape simulation, the method of approximate mainly confined to the computer science failed to rise and computing power co., LTD. The calculation formula of gear meshing stiffness is obtained by simplifying the calculation of the comparison between elastic deformation and load action in all directions. Fig. (b) further improves the Ishikawa method model, and proposes the analysis model of cantilever beam with variable section based on the gear base circle.
Since this model is based on the base circle, the tooth root circle and the base circle may not coincide completely according to the formation principle of gear tooth profile. When the tooth root circle is smaller than the base circle (Fig. (a)), the part between the tooth root circle and the base circle is not considered. When the tooth root circle is larger than the base circle (Fig. (b)), the part between the tooth root circle and the base circle is more considered for calculation. Only when the tooth root circle and the base circle coincide, the accuracy of the tooth calculation model is reliable. It can be seen that using this model to calculate the gear tooth meshing stiffness will lead to the existence of errors, and the farther the distance between the base circle and the tooth root circle is, the greater the calculation error will be. Wan Zhiguo et al. optimized and revised the less calculation and more calculation parts of this mesh stiffness algorithm, and compared it with the improved IS06336, the results show that the proposed correction formula has certain reliability and effectiveness. With the further study of the meshing stiffness and the updating of the algorithm, the calculation model of the actual gear tooth profile with the combination of the actual involute tooth profile and the fillet transition curve as shown in Fig. (c) was proposed.
The calculation and application of the detailed actual involute tooth profile model proposed in Fig. (c) have been studied and verified by many researchers. Sainsot et al. applied the fillet Angle/matrix flexibility analysis to the calculation of circular elastic ring based on the Muskhelishvili theory and proposed a statistical formula for the calculation of matrix stiffness. The reliability of the result of this algorithm is better than that of Webei method, especially it is very effective for the features of multiple teeth or large gears. Zhou et al. ML used the involute tooth profile model with variable cross-section to calculate the time-varying meshing stiffness of the gear pair by applying the crack propagation simulation path, and also considered the deformation of the gear wheel body. Finally, a 16DOF dynamic model of the gear system was established to study the dynamic response of the system, and the influence of meshing stiffness and crack growth on the system response was studied. Pandya et al. realized the efficiency of high contact ratio (HCR) gear transmission by appropriately selecting the gear geometry to improve the load capacity and achieve smooth operation. Compared with low contact ratio (LCR) gear, the calculation of the mesh stiffness of HCR gear is a little more complicated due to the large number of average contact gears at a given time. The potential energy model was used to estimate the meshing stiffness according to the effect of the backgap ratio and pressure Angle parameters.
