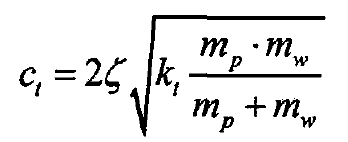Taking the basic parameters of gear pair 1 as an example, it is difficult to use regular geometric algorithm to calculate the mass and moment of inertia of gear due to the non-linear geometric particularity of gear tooth profile. In order to reduce the uncertainty of the system input parameters and improve the accuracy of the basic parameters of the system, the corresponding two-dimensional plane geometry is established according to the tooth profile piecewise equations (fillet curve AB and involute curve BD) derived in this paper, and then the corresponding three-dimensional mathematical model (as shown in the figure) is constructed in the three-dimensional modeling software according to the two-dimensional geometry, and the corresponding gear material density is input and calculated The mass, moment of inertia and other parameters of the corresponding gear are calculated.

According to the above calculation conversion method, the relevant system input parameters after gear calculation, including other relevant support, torsional stiffness or damping parameters of the system.

According to the meshing stiffness excitation and damping characteristics of gear pairs in the system, the following relevant calculation and setting are carried out. The stiffness excitation of the system adopts the research results of time-varying meshing stiffness in Chapter 2 and Chapter 4 as the input analysis parameters, which includes two categories: meshing stiffness without pitting and meshing stiffness with pitting. The related meshing stiffness derivation process will not be repeated here. For the characteristics of gear meshing damping in the system, the formula is used to calculate and study, in which the damping is proportional to meshing stiffness and gear mass. When the symbol ζ is set as damping ratio, in the research results of relevant scholars, the damping ratio is generally in the range of 0.01-0.1.