The obtained normal curvature and short-range torsion Aa1, BA1 and CA1 are along the direction of EA1 and TA1. Let the normal curvature of the pinion tooth surface along the EF1 direction at the calculation point be AF1, the short-range torsion be CF1 and the normal curvature along the TF direction be BF1. It is obtained by Euler formula and Bertrand formula:

Let the contact line direction angle of the small wheel and the production wheel at the node be ω 2. From the wheel blank design:

EF1 and TF are the two main directions of the nodes on the profile tooth surface of the small wheel, and the generating curvature A01 of the profile wheel along EF1 direction is set, τ Is the forming radius of point m on the cutter head. Because EF1 is the main direction of the cutter head, the short-range torsion in this direction C01 = 0. TF is the generatrix direction of the cutter head, and the principal curvature B01 in this direction = 0. In this way, the induced normal curvature and induced short-range torsion of the forming wheel and the small wheel along the EF1 and TF directions are respectively:

According to the gear meshing principle in Chapter 2:
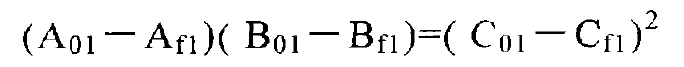
Namely:

Thus, the forming radius of the calculated point can be solved:

