In order to reflect the influence rule of parameters on the maximum circumferential stress, dimensionless radius of chamfered root of flexible gear is converted into coefficient of radius of chamfered root r4=r4/m, dimensionless thickness h of ring gear is converted into coefficient of ring wall thickness h=h/m, dimensionless maximum circumferential stress of ring gear is converted into maximum circumferential stress divided by u0Eh/rm2.
1. Effect of radius of chamfered root on circumferential stress
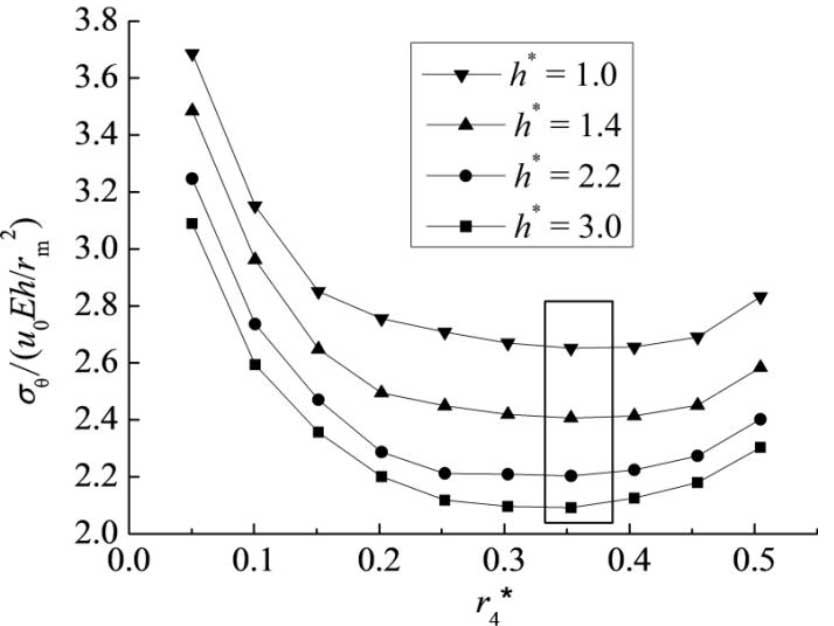
Figure 8 shows that the maximum circumferential stress of the ring gear changes with the radius of the root chamfer when h* is taken as 1.0, 1.4, 2.2 and 3.0 respectively. As the radius of the root chamfer increases, the maximum circumferential stress first decreases significantly and then increases slightly. The rightmost end of the curve is shown as the maximum radius of the root chamfer. The larger the radius of the root chamfer, the more conducive to reducing the stress concentration in the groove area;Increasing the radius of chamfered root will increase the bending rigidity of the ring gear and increase the internal force and bending stress of the ring gear. The calculation shows that the radius of chamfered root is not the bigger the better. In order to reduce the maximum stress of the groove, the optimum radius of chamfered root is about 0.36m. The maximum circumferential stress discussed below is the maximum circumferential stress of the groove when the optimum radius of chamfered root is the optimum radius of the ring gear (data).
The influence of gear teeth on the maximum circumferential stress of the ring gear is reflected in the increase of bending rigidity and stress concentration. To further study the influence of gear teeth on the increase of circumferential bending rigidity and stress concentration of the ring gear, the definition is:
(a) The tooth stress influence coefficient KT is the ratio of the maximum circumferential stress of the toothed finite element model to the stress theoretical value of the aperture model;
(b) The bending stiffness increase factor Ktr is the ratio of the roller thrust to the theoretical value of the roller thrust of the toothed finite element model;
(c) Stress concentration factor: KC= KT/ Ktr.
Compare the Ktr of the finite element model with YZ of Formula (6) and Krt of the design specification to discuss the influence rule of gear teeth on the bending rigidity of the ring gear. Compare the stress concentration coefficient KC with the K of the design specification and discuss the variation rule of the stress concentration coefficient.
2. Variation regularity of increasing coefficient of bending stiffness
The slot width ratio is v=1, 1.2, 1.4 and 1.6 respectively. The variation rule of Ktr of finite element model and YZ of reference [4] and Krt of design specification with h* is shown in the figure. When h* increases from 1.0 to 3.0, the increase coefficient of tooth stiffness obtained by the three methods decreases with the increase of ring wall thickness; the increase coefficient of bending stiffness of finite element model decreases with the increase of slot width.
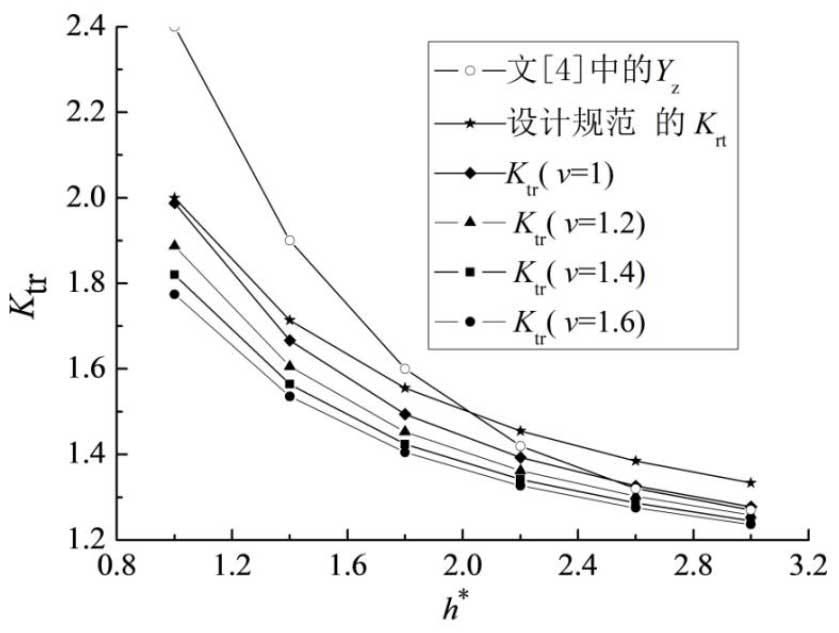
The deviation between finite element model results and YZ in literature [4] is large, and Krt deviation from design specification is small, but both of them are larger than the increase coefficient of bending rigidity of finite element model, indicating that they overestimate the influence of gear teeth on the bending rigidity of ring gear; with the increase of h*, the deviation between finite element model results of v=1 and YZ is reduced from 17.2% to -0.6%, and the deviation from design specification is increased from 0.6% to 4.6%.2%.
3. Variation regularity of stress concentration coefficient of gear teeth
The variation rule of stress concentration coefficient KC and K of design specifications with ring gear wall thickness is shown as V taking 1, 1.2, 1.4 and 1.6.
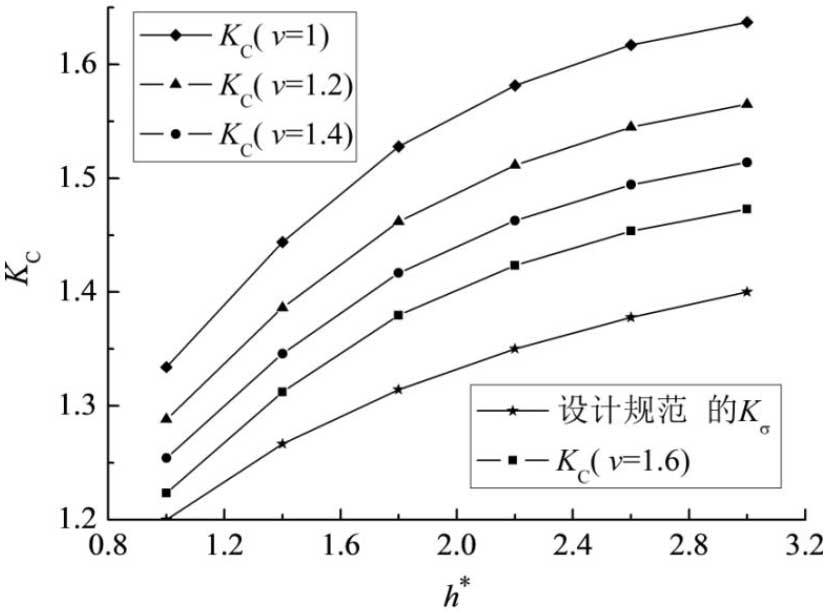
As shown in the diagram, the stress concentration coefficient of the gear teeth increases with the thickness of the ring gear and decreases with the width of the groove. The K of the design specification is lower than that of the finite element model; it shows that the K of the design specification underestimates the influence of the gear teeth on the stress concentration. As the thickness of the ring gear increases, the deviation between the finite element model result of v=1 and the K increases from 11.2% to 16.9%.
