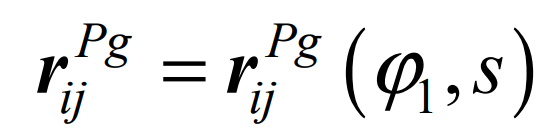The traditional tooth surface contact mainly includes transmission error and tooth surface contact area. At present, a new analysis method, tooth surface mismatch, is added. Generally speaking, when the macro geometry of a pair of tooth surface pairs is determined, its meshing performance is basically determined by the micro geometry of the tooth surface. The tooth surface mismatch reflects the deviation of the tooth surfaces of the large and small gears of the spiral bevel gear from the conjugate tooth surface, including various modification information of the two meshing tooth surfaces (tooth profile modification, longitudinal modification, tooth surface distortion and high-order modification), It can directly reflect the micro geometry and meshing characteristics of the matched tooth surface (especially the size and position of contact spots, contact stress, motion error and installation error sensitivity). Therefore, tooth surface mismatch has increasingly become an important part of tooth surface contact analysis.
There are two methods for tooth surface mismatch design: one is based on the tooth surface mismatch design of spiral bevel gear, which is compared between the conjugate tooth surface of spiral bevel gear and the theoretical tooth surface of small gear; The other is based on the mismatch design of spiral bevel gear and large gear surface, which is compared between the conjugate tooth surface of spiral bevel gear and the theoretical tooth surface of large gear. The tooth surface mismatch diagram can directly reflect the tooth surface shape and mismatch of spiral bevel gear, and has become one of the important contents of tooth surface contact analysis of spiral bevel gear. Because the tooth surface of small gear is seriously distorted due to its small number of teeth and large helix angle (hypoid gear), it is difficult to compare the conjugate tooth surface of spiral bevel gear with that of small gear; Compared with the theoretical tooth surface of the large wheel, it is much easier to compare the conjugate tooth surface of the small wheel with the theoretical tooth surface of the large wheel.
The general solution process of the second tooth surface mismatch design method is: the large tooth surface equation is obtained from the meshing between the generating surface of the large spiral bevel gear and the large tooth surface, the small wheel tooth surface equation is obtained from the meshing between the generating surface of the small spiral bevel gear and the small wheel tooth surface, and then the conjugate tooth surface equation of the small wheel is obtained from the tooth surface equation of the small spiral bevel gear, Finally, the tooth surface mismatch is calculated by comparing the conjugate tooth surface of spiral bevel pinion with that of large gear.
The new method is based on the mismatch design of spiral bevel gear and large gear surface. The specific calculation process is as follows. From the machine tool adjustment parameters of the large spiral bevel gear, the profile wheel equation of the large gear can be obtained as follows (Fig. 1).
Where, ϕ 2 is the cutter head angle, which is the parameter of the production surface. The superscript GG represents the generating surface of the spiral bevel gear, and the subscripts I and j represent the row and column numbers of the tooth surface grid points. When the tooth surface grid is divided into M rows and N columns, I ∈ (1, m), J ∈ (1, n).
When the spiral bevel gear wheel is processed by the generating method, the gear tooth surface equation can be obtained from the meshing equation between the generating wheel and the gear tooth surface as follows:
When the large spiral bevel gear is processed by the forming method, the tooth surface equation of the large gear is equal to the tooth surface equation of the generating surface of the large gear:
According to the machine tool adjustment parameters of the spiral bevel pinion, the production surface equation of the pinion can be expressed as follows (Fig. 2):
Where, the superscript PG represents the generating surface of spiral bevel pinion, ϕ 1 and s are the tooth surface parameters of spiral bevel pinion. Because the generating surface of the small wheel is completely conjugate with the tooth surface of the small wheel, the tooth surface mismatch is obtained by comparing the generating surface equation of the small wheel with the large tooth surface, which is equivalent to the tooth surface mismatch obtained by comparing the conjugate tooth surface of the small wheel with the large tooth surface. The design result of tooth surface mismatch is:
Where, superscript EO indicates tooth surface mismatch.
The method omits the calculation process of obtaining the small wheel tooth surface from the generating surface of the spiral bevel small wheel, and then obtaining the conjugate tooth surface of the small wheel from the spiral bevel small wheel tooth surface, which greatly simplifies the calculation and obtains the same tooth surface mismatch design results.