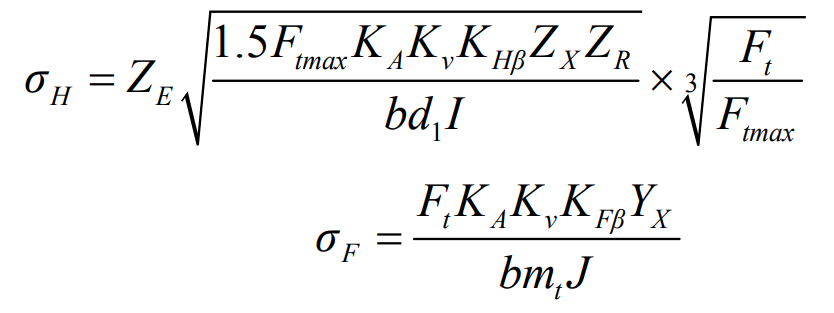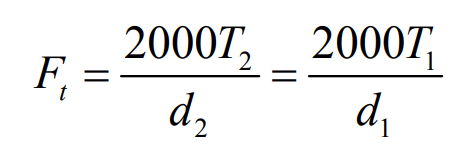In order to further analyze the tooth surface contact stress and tooth root bending stress of spiral bevel gear under specific working conditions, the stress calculated by finite element method is compared with the calculated value of theoretical formula. The theoretical calculation formulas of tooth surface contact stress and tooth root bending stress of spiral bevel gear are as follows:
In the formula, σ H is the calculated contact stress, σ F is the calculated bending stress; Ze is the elastic coefficient, the maximum tangential force in the operation of ftmax small wheel, Ka service coefficient, kV dynamic load coefficient, K H β Calculation of bearing capacity of tooth surface in X direction, calculation of bearing capacity of tooth surface in Z direction
Coefficient, B tooth width, 1D is the diameter of the indexing circle of the small wheel, and I is the geometric coefficient for calculating the contact stress of the tooth surface; KF β Is the tooth load distribution coefficient, YX is the size coefficient, MT is the modulus of the end face of the big end, B is the tooth width, j is the geometric coefficient, and FT is the tangential force acting on the indexing circle of the big end.
In the formula, T1 and T2 are the torque of small wheel and large wheel respectively. D1 and D2 are the diameter of the indexing circle at the big end of the small wheel and the big wheel respectively.
According to the low speed and slight vibration working condition of spiral bevel gear simulated in the static contact analysis, the coefficients in the calculation formula of tooth surface contact stress and tooth root bending stress of spiral bevel gear are the same under each working condition.