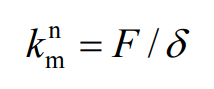In the dynamic modeling and analysis of hypoid gear system, the meshing relationship of hypoid gear is treated as spring damping element. The excitation force of hypoid gear meshing element caused by transmission error is the main cause of system vibration and noise. Therefore, obtaining accurate hypoid gear meshing parameters is the basis of system dynamic analysis. Scholars at home and abroad have done a lot of research on the calculation of meshing parameters of cylindrical gears with parallel shafting, but there is less research on hypoid gears with vertical shafting and offset. Hypoid gear is widely used in the transmission system of main reducer of drive axle. It has more complex geometric characteristics and meshing characteristics than cylindrical gear. Because its meshing state changes periodically with time, it is necessary to accurately consider the time-varying characteristics of meshing parameters of hypoid gear when establishing the meshing model of hypoid gear. Some scholars used the method of surface integral and finite element synthesis to analyze the loaded contact of hypoid gear, and calculated the time-varying meshing parameters of hypoid gear. This method assumed that the contact area of hypoid gear was semi elastic space, used the Boussinesq curved area method to calculate the contact, and the deformation of non-contact area was obtained by the finite element method, Because the range of contact area is set artificially, the calculation accuracy of this method is affected by the division of contact area and non-contact area.

The finite element contact analysis method can accurately simulate the contact state of hypoid gear, but the existing research mainly uses the finite element method to check the strength of hypoid gear, and there is less research on the meshing parameters of hypoid gear. Some scholars use the finite element method to calculate the meshing stiffness of spiral bevel gears. First, the single tooth meshing stiffness is obtained by the ratio of the normal contact force of a single tooth to the comprehensive elastic deformation of a single tooth, and then the multi tooth meshing stiffness is obtained by linear superposition of the single tooth meshing stiffness. Because the hypoid gear has unusually complex geometric characteristics, The equivalent normal contact force and comprehensive elastic deformation direction of each meshing gear pair are different, so it is not accurate to obtain the multi tooth meshing stiffness directly from the linear superposition of single tooth stiffness.

In addition, most of the existing scholars use the calculation formula of the ratio of force to deformation when calculating the meshing stiffness of hypoid gears:

Where:

F – equivalent meshing force;

δ —— Equivalent deformation.

The stiffness knm obtained by the formula is the secant stiffness. It can be seen from the relationship curve between meshing force and deformation of hypoid gear in the figure that the contact of hypoid gear has nonlinear stiffness characteristics. When the hypoid gear reaches equilibrium under a certain load, the actual meshing stiffness should be the tangent stiffness under this state.

Where

DF — small variation of equivalent meshing force along the action direction of meshing force when hypoid gear is balanced;

d δ —— Small deformation in the corresponding direction.

It can be seen that the tangent stiffness KTM is greater than the secant stiffness knm, so it is inaccurate to use the secant stiffness to analyze the dynamics of the system.

In view of the shortcomings of the existing research methods, a method for accurately calculating the time-varying equivalent meshing parameters of hypoid gear is proposed. The load contact calculation of hypoid gear is carried out by using the general finite element software ABAQUS, the time-varying equivalent meshing parameters of hypoid gear are obtained, and the variation characteristics of time-varying meshing parameters under different torque are further studied. The correctness of the modeling and calculation in this paper is verified by comparing with the transmission error curve of classical hypoid gear contact analysis (TCA) and loading meshing imprinting test. The obtained time-varying meshing parameters lay a foundation for the dynamic analysis of hypoid gear system.