The influence of stiffness excitation is directly reflected in the time-varying coefficient of elastic force term in the dynamic model equation. As a parametric excitation, it plays an important role in the process of gear transmission.
The comprehensive meshing stiffness (kkmm) of non-circular gear is a periodic time-varying function, which is expressed by Fourier series
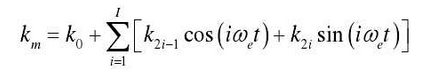
It can be seen from the process of creating the geometric model of reducer variable speed integrated gear that the profile shape of non-circular gear is very complex, and it is difficult to solve the meshing stiffness by theoretical calculation. Therefore, in this paper, the tooth profile model of non-circular gear is constructed by UG, and then the stiffness of tooth is obtained by finite element analysis. Firstly, the data points of the tooth profile are obtained by the non-circular gear profile model, and then the tooth profile surface is generated in the 3D software, and then the 3D tooth model of the non-circular gear is obtained. The small cylindrical gear is a standard involute gear, which can be directly generated in 3D software.
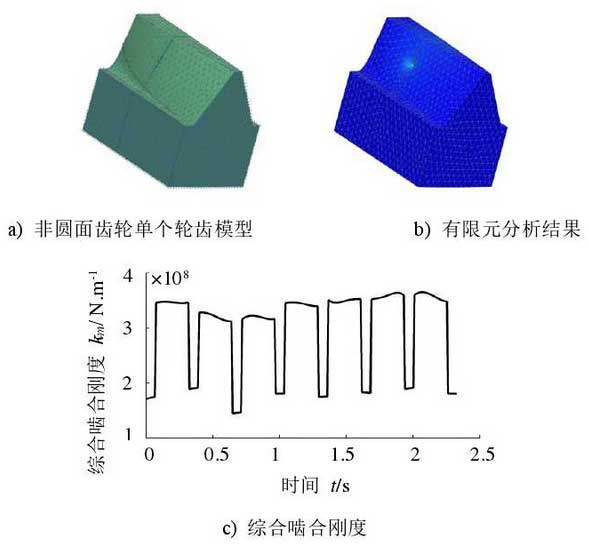
The single tooth in the three-dimensional model of cylindrical gear and non-circular gear is extracted as the research object, and the finite element analysis is carried out. The tooth stiffness is calculated by finite element method, and the finite element calculation model of single tooth stiffness of non-circular gear is given in Fig. a). The non-circular gear is point meshed, and the unit normal force is applied on the meshing point. The deformation of the tooth can be obtained by finite element calculation, as shown in Fig. b). The single tooth stiffness K at the meshing point can be obtained by extracting the deformation s at the meshing point and K = 1 / s. By changing the position of the meshing point, the corresponding stiffness is calculated, and the stiffness curve of single tooth is obtained by fitting the obtained data. In the same way, the single tooth stiffness curve of the cylindrical gear can be calculated, and the meshing stiffness curve of a single pair of teeth can be obtained by treating the two teeth as a series spring. Then, according to the coincidence degree in the meshing process, the comprehensive meshing stiffness kkkm km of the non-circular gear in the whole rotation cycle is calculated, as shown in Fig. C). Due to the different teeth of non-circular gears and the non-uniformity, the comprehensive stiffness values of each cycle are different. The parameters K0, k2i-1 and k2i can be obtained by discrete Fourier transform.
