The meshing stiffness of spur bevel gears is an important parameter that affects the load capacity and dynamic characteristics of gears. The meshing stiffness of straight bevel gear mainly adopts the Tredgold approximation, that is, the tooth profile of straight bevel gear is simplified into countless infinitesimal approximate solutions along the tooth width direction by using the finite element method. Based on the research of Lafi et al., the stiffness of gear tooth matrix is introduced and the calculation model of meshing stiffness of straight bevel gear is established.
The meshing stiffness ko of the micro-element gear includes Hertz contact stiffness kho, tooth matrix stiffness kfo, bending stiffness kbjio, axial compression stiffness kajio, shear stiffness ksjio (i=1,2; j=p, g), which can be obtained from the formula respectively.
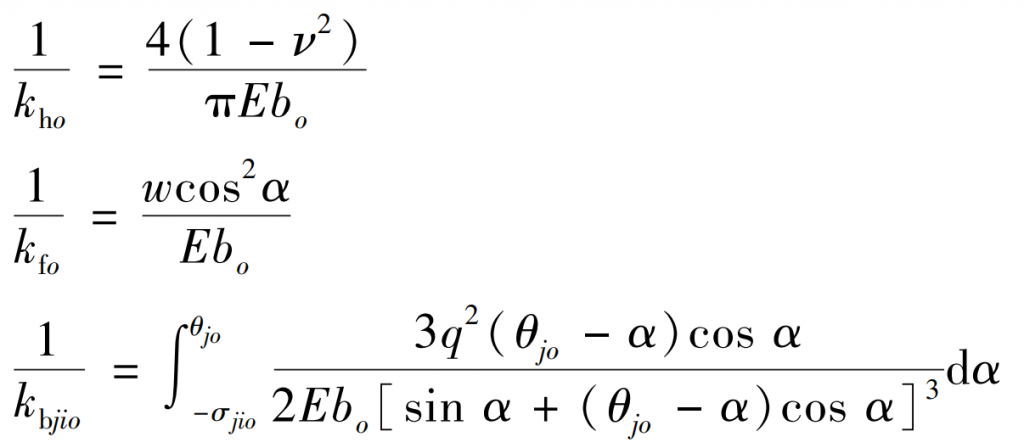
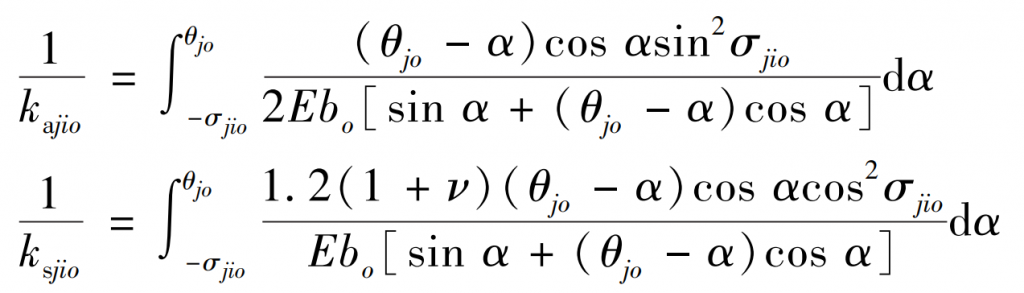
Where: E and ν Young’s modulus and Poisson’s ratio; σ Jio is the included angle between the meshing line of the o th micro-element gear and the tooth centerline along the tooth width direction; θ jo = 0. 5π/ zjo + inv α Is the half value of the tooth angle of the o th infinitesimal gear along the tooth width direction; Nj is the number of micro-element gears along the tooth width direction; The meshing stiffness of straight bevel gears can be obtained by the formula.
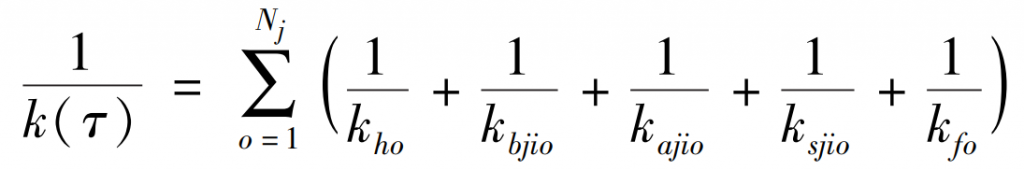
According to the coincidence degree, the tooth profile meshing area can be divided into single-tooth meshing area BC, double-tooth meshing area AB and CD. Then the meshing time of single/double teeth of straight bevel gear is tAB=tCD=( ε m - 1)T0 ,tBC = (2 - ε m) T0, where T0=tAC=2 π /( ω PzP) is the alternating time of single and double teeth. It is assumed that the meshing stiffness of the tooth back contact is the same as that of the tooth surface meshing. The meshing stiffness of the straight h-tooth straight bevel gear pair shown in the table is as shown in the figure.