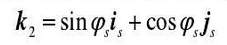When machining non-circular gear, the relative velocity before two gears is perpendicular to the normal vector of the meshing contact point according to the condition of correct meshing. Therefore, the meshing equation can be expressed by the relative velocity between the two gears at the meshing point and the unit normal vector of the tooth surface of the cutter
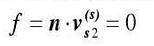
Where, the relative velocity vector (M / s) at the tangent point of two gear tooth surfaces.
If the above meshing point is set as a point L on the cutter tooth surface and expressed as a vector in the coordinate system SS, then the vector diameter rs of point L is:
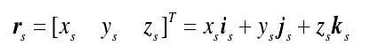
If the angular velocities ω s and ω 2 are assumed angular velocities of point L in the coordinate systems SS and S2, respectively, then the velocity vectors vs and V2 are:
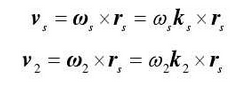
The vector difference between velocity vs and V2 is VS2. Then the VS2 of G point can be expressed as follows:
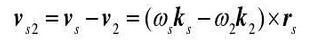
In the formula, there are unit vectors in different coordinate systems. K2 is expressed by the unit vector in the coordinate system SS through the space coordinate transformation matrix M2S. Thus, the equation of the relative speed of the two gears in the coordinate system SS is obtained