In the actual machining of the end face spiral gear coupling, due to the influence of machine tool thermal deformation, elastic deformation, axis movement error, fixture error and other factors, the actual tooth surface processing has tooth profile error. By using the gear measuring center, the actual tooth surface of workpiece can be measured according to the spatial coordinates and normal vectors of each discrete point on the theoretical tooth surface, and the tooth profile error value of the actual tooth surface relative to the theoretical tooth surface can be obtained. According to the tooth surface equation, the tooth surface shape of the end face spiral gear coupling is determined by the adjustment parameters of the machine tool and the grinding wheel. Therefore, the tooth profile error can be corrected by changing the machine tool adjustment parameters and the grinding wheel parameters, so that the actual machined tooth surface is consistent with the theoretical tooth surface.
Let the theoretical tooth surface equation be R2 = R2 (A1, A2 , an), where AJ (J = 1,2 , n) is a parameter variable, i.e. machine tool adjustment parameters and grinding wheel parameters. The tooth profile error at any point on the tooth surface can be considered as the superposition of the tooth profile error caused by the small changes of machine tool adjustment parameters and grinding wheel parameters Δ AJ. In order to modify the parameters to minimize the error of each point as far as possible, based on the 9 × 5 mesh divided by the tooth surface, 45 points on each side and 90 points on the left and right tooth surfaces, the radial vector r2i and normal vector n2i (I = 1, 2,…) of each point are calculated ,90)。 After the parameter is modified, for each point, the equation is
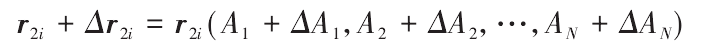
There are 90 points on the tooth surface
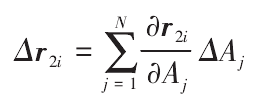
Its projection length on the normal vector of the corresponding point is
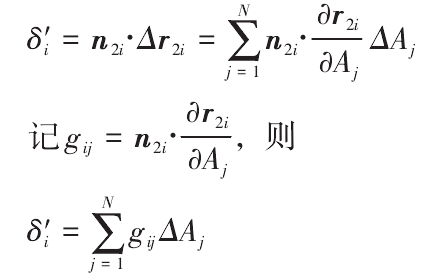
In order to correct the original tooth profile error δ I of each point on the actual tooth surface, it is necessary to minimize | δ ‘I + δ I |. Considering the whole tooth surface, a function is constructed
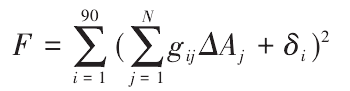
As long as the appropriate Δ AJ (J = 1,2 When the above function reaches the minimum value, the required correction value Δ AJ can be obtained. Therefore, the partial derivative of F with respect to Δ AJ can be obtained and made to be 0
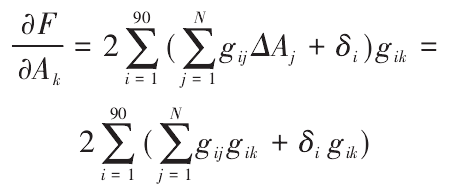
Where k = 1, 2 ,N。 From equation (13), a linear system of equations about Δ AJ can be obtained
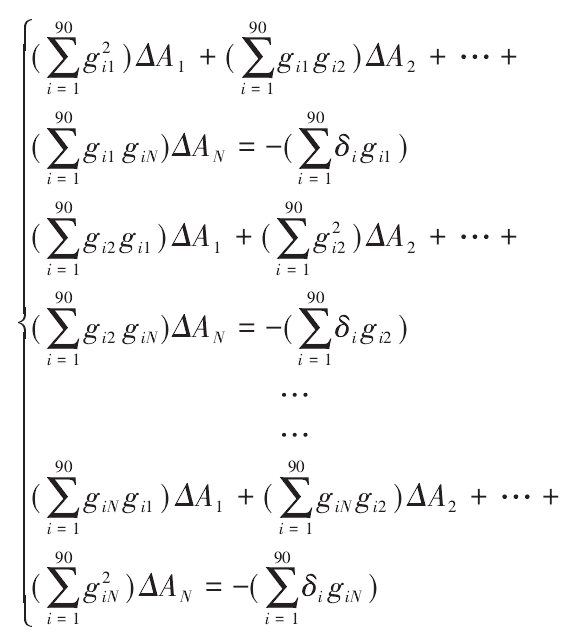
The formula can be written in the matrix form of AX = B, and the required modified parameter Δ AJ can be obtained by solving the linear equations.
When solving the linear equations AX = B, the condition number cond (a) is too large, which leads to the small perturbation of a and B, which will cause large error of the solution, so it is determined that the system is ill conditioned. In order to obtain reasonable results, Tikhonov regularization and L-curve method are used to transform AX = B into (β I + ATA) x = ATB
Taking log ∥ x ∥ 2 as x-axis and log ∥ ax – B ∥ 2 as y-axis, the L-curve is made, and the point β 0 with the largest curvature on the L-curve is taken and substituted into the formula to obtain the optimal solution. The method can effectively solve the linear equations, and get the adjustment parameters of machine tool and grinding wheel to correct the tooth profile error.
Since the concave and convex teeth of the end face spiral gear coupling are processed by different machine tool adjustment parameters and grinding wheel parameters, the tooth profile errors of the concave and convex teeth should be corrected respectively. Combined with the tooth surface equation of end face spiral gear coupling, the machine tool adjustment parameters and grinding wheel parameters that can be used for tooth profile error correction mainly include radial cutter position s, bed XB2, nose radius RG, cutting edge pressure angle α, tooth profile modification radius RHB.
