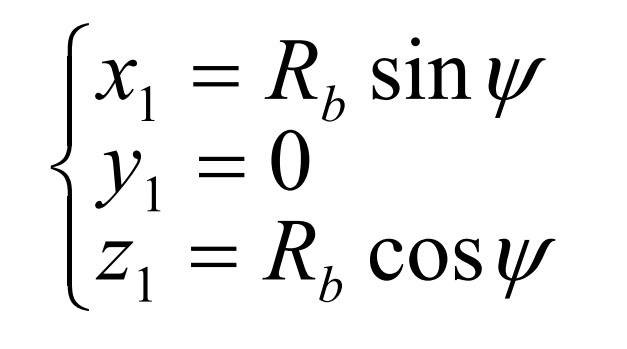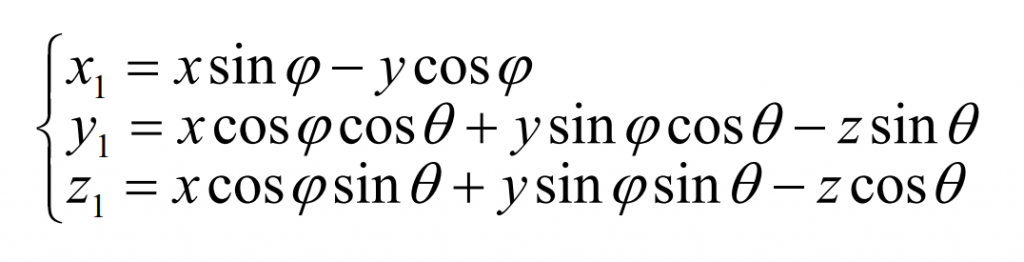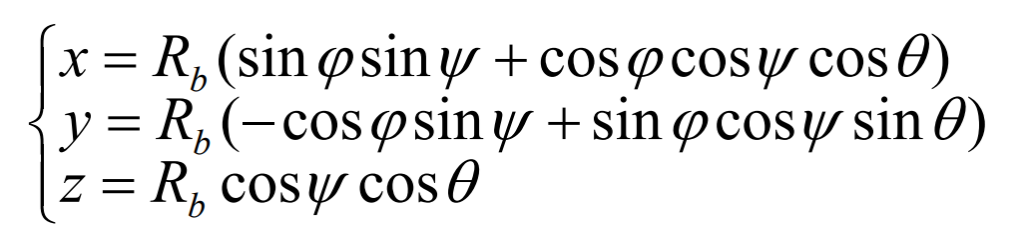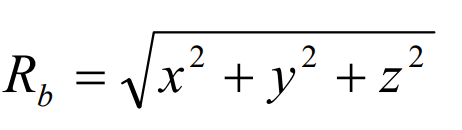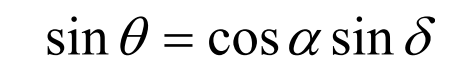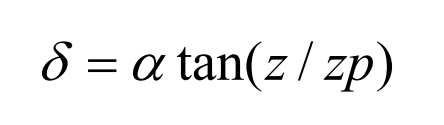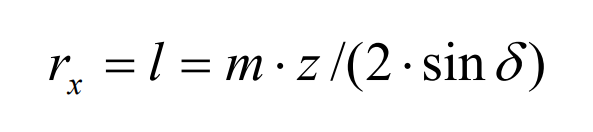The motion form of cylindrical gear pair transmission is pure rolling based on cone, while the motion of a pair of meshing bevel gears is spatial spherical motion. Therefore, the tooth profile theory of bevel gear is a complex spatial curve, that is, spherical involute. Because the spherical surface is a non deployable surface, it is difficult to design, process and test. The traditional design method is to use the plane involute approximation to replace the spherical involute tooth profile, and this approximate design method affects the design accuracy of hypoid gear and reduces its application performance to a certain extent. Starting from the formation principle of spherical involute, this section studies the basic characteristics of spherical involute in detail, deduces the spherical involute formula, obtains the spherical involute tooth profile by using the method of generating curve from equation in Pro / E, and strives to obtain a relatively accurate modeling method of hypoid gear.
(1) Forming principle of spherical involute
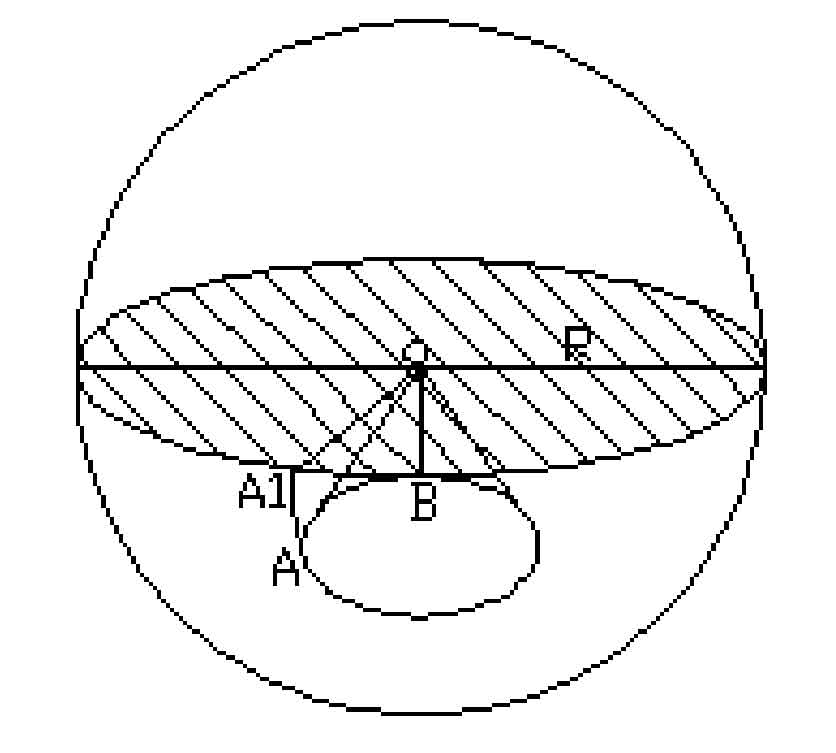
As shown in Figure 1, a circular plane is tangent to a base cone, the center O of the circular plane coincides with the apex o of the cone, and the radius r of the circular plane is equal to the length of the cone bus. The circular plane rolls along the base cone. From the initial position tangent to the base cone bus OA to the position tangent to the base cone bus ob, the locus of point a on the circular plane is the spherical involute, as shown in Figure 1, and curve Aa1 is the spherical involute generated by point a. The tooth surface of hypoid gear is composed of a group of spherical involutes with cone apex o as the spherical center and different radii. When the circular plane rolls along the conical surface, the locus of the radius tangent to the cone at the initial position of the circular plane is the spherical involute surface.
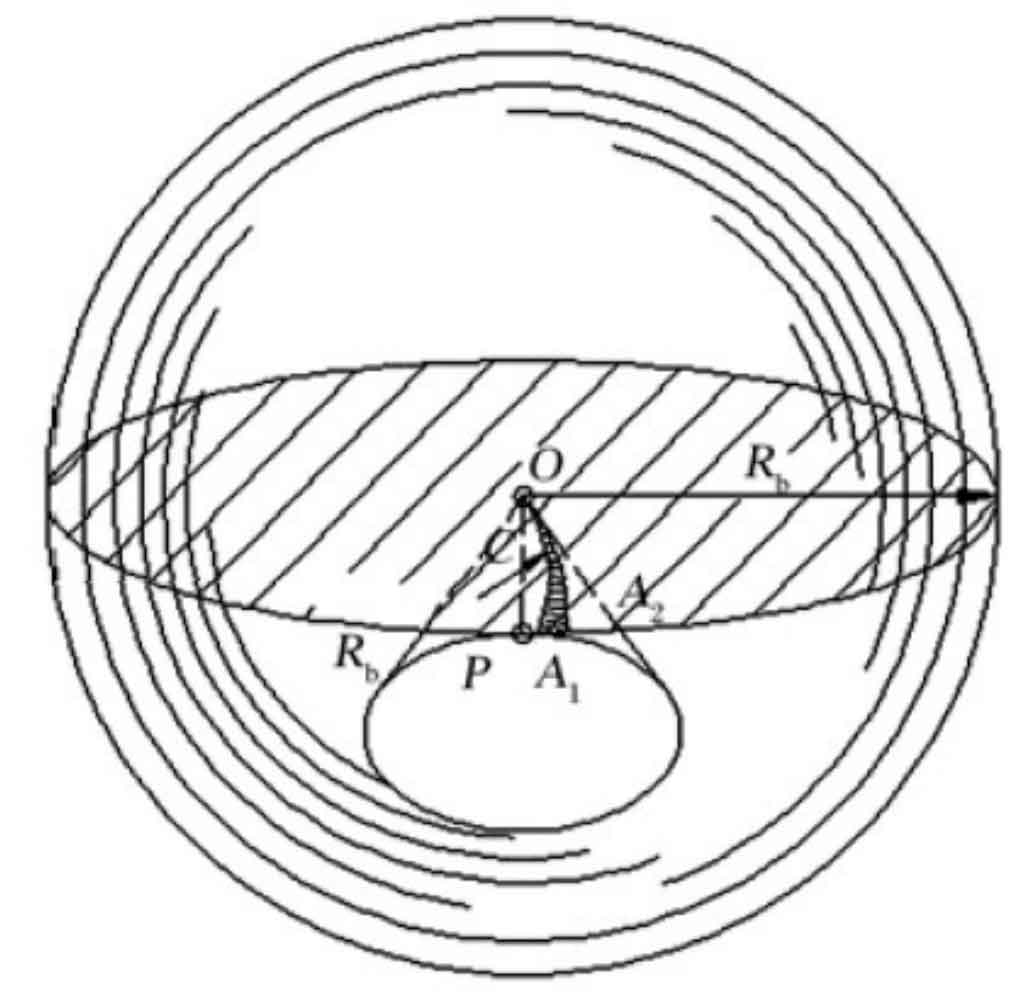
When the above tangent radius is changed into a circular arc, when the circular plane is pure rolling along the base conical surface, the curved surface formed by taking the circular arc as the generating line is the theoretical tooth profile of the hypoid gear, and Figure 2 is the formation principle of the tooth profile of the hypoid gear.
(2) Derivation of spherical involute formula
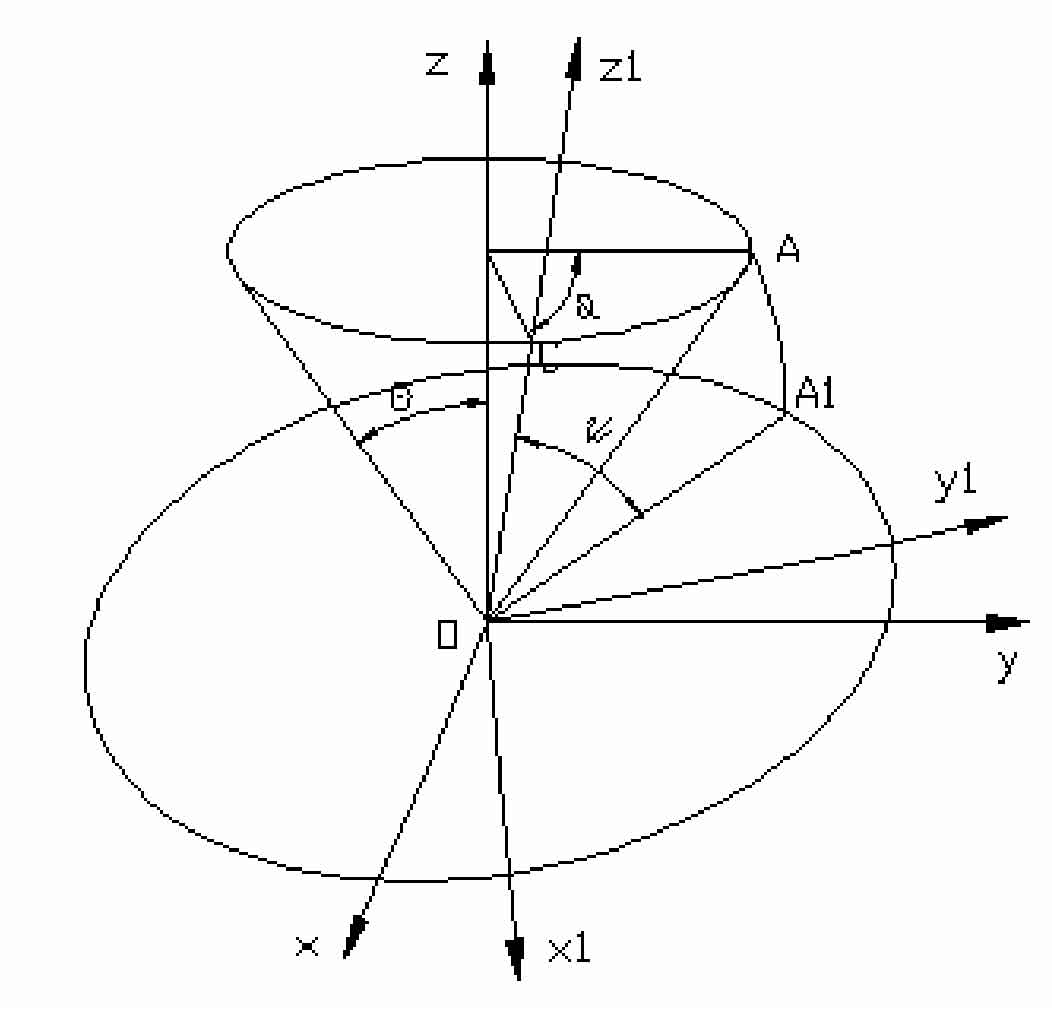
According to the generation theory of spherical involute, spherical involute is a curve located on the surface of the ball. As shown in Figure 3, a fixed rectangular coordinate system (x, y, z) is established with the vertex o of the base cone as the origin and the straight line of the height of the base cone at the o point as the Z axis. A moving coordinate system (x1, Y1, z1) is established with the vertex o of the base cone as the origin, the OC direction of the base cone bus as the Z1 axis, and the straight line passing through the o point perpendicular to the Z1 axis in the circular plane as the X1 axis. In the moving coordinate system, the trajectory equation of point a is:
Where, Rb represents the outer cone distance, that is, the radius of the circular plane; Ψ Is the angle between OA and 1z axis.
The spherical involute is formed by a point a on the pure rolling plane of the circular plane along the base cone relative to the base cone, that is, relative to the fixed coordinate system (x, y, z). Therefore, the conversion formula of the two coordinate systems can be obtained:
In the formula, θ Is the base cone angle; φ Angle the circular plane.
The spherical involute equation of hypoid gear can be obtained by transforming the trajectory equation of point a into two coordinate transformation formula as follows:
In the formula, cone distance:
From the sine formula of spherical geometric trigonometric relationship:
The hypoid gear pair with shaft intersection angle Σ = 90 ° can be obtained from the determined geometric model:
Pitch cone angle:
Cone pitch: