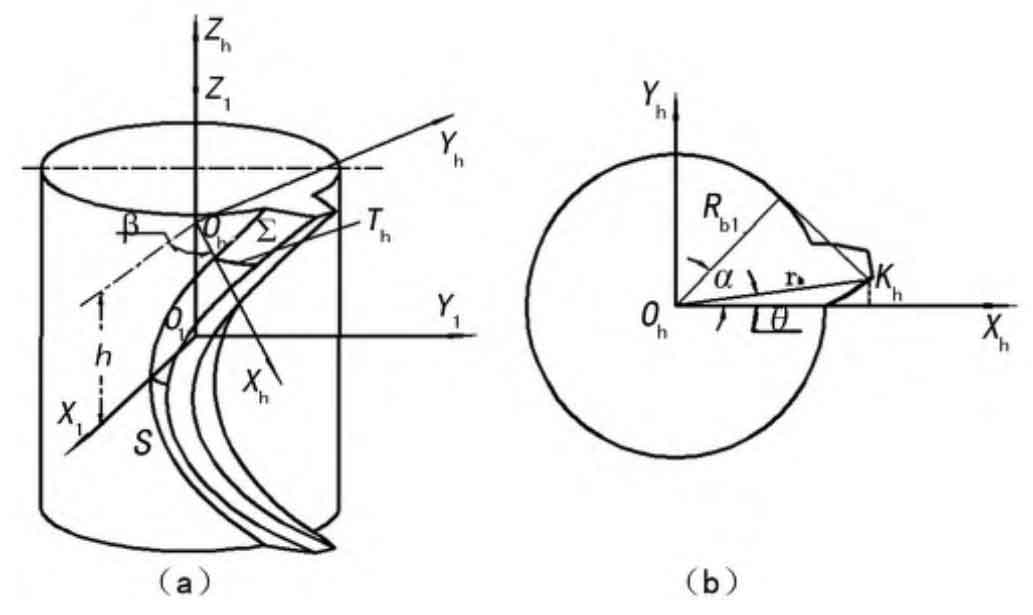
As shown in Figure (a), the tooth surface Σ of circular tooth profile cylindrical gear can be considered to be formed by scanning the involute tooth profile T of a certain radial section tooth surface along the base cylindrical tooth profile S. Establish a coordinate system at the middle section of the base cylinder, so that the X1O1Y1 plane of S1 (X1Y1Z1) passes through the middle section of the base cylinder, Z1 passes through the axis of the base circle, and the radius of the base circle is Rb1. The coordinate system Sh (Xh Yh Zh) is the position coordinate system of the circular tooth line cylindrical gear tooth line from the middle section h, β Is the position angle of the spiral tooth line. The section between the gear tooth and the plane XhOhZh is shown in Figure (b). The intersection Th of the gear tooth and the tooth surface Σ is an involute.
The involute equation of the tooth profile of circular tooth profile cylindrical gear is:
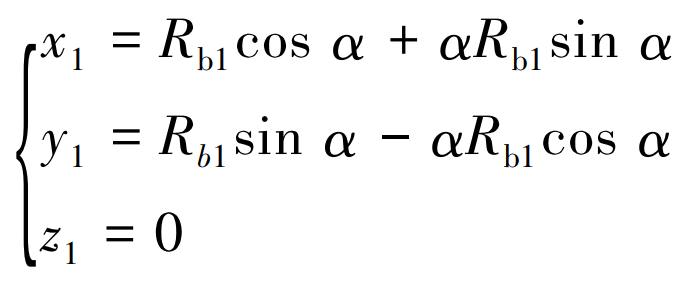
Where: α Unfold the angle for the involute.
Z1 and Zh are coaxial and both pass through the base cylinder axis. The circular tooth profile of the plane XhOhZh section of the cylindrical gear can be considered as the involute tooth profile on the X1O1Y1 plane rotating around the Z axis β It is obtained that the equation of involute under the coordinate system Sh is:
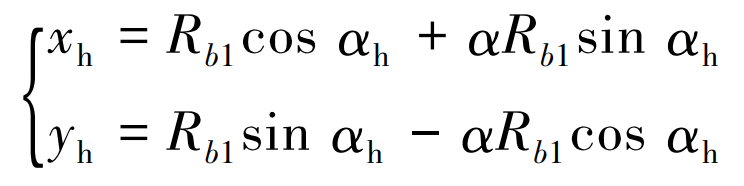
According to its geometric relationship, the position angle of arc tooth line can be deduced as follows:
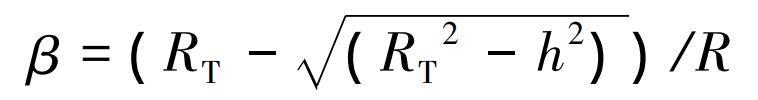
Where: R is the radius of the graduation circle; RT is the radius of circular tooth line of cylindrical gear.
The transformation matrix from Sh coordinate system to S1 coordinate system is:
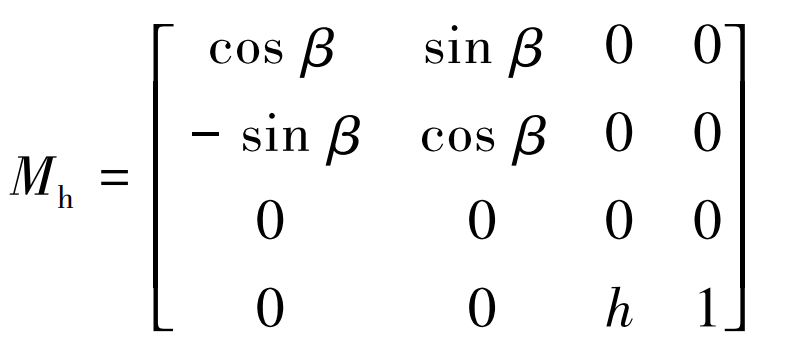
Through coordinate transformation:
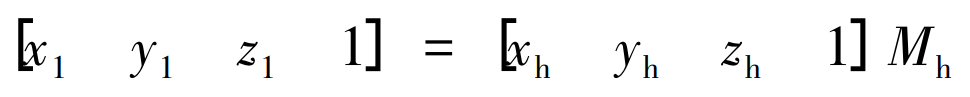
The tooth surface equation of cylindrical gear with circular tooth profile can be derived:
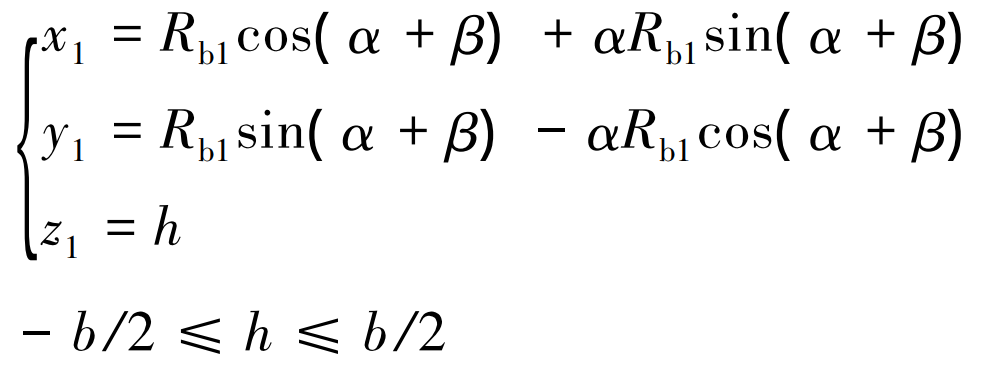
Where: b is the tooth width of cylindrical gear with circular tooth profile.
