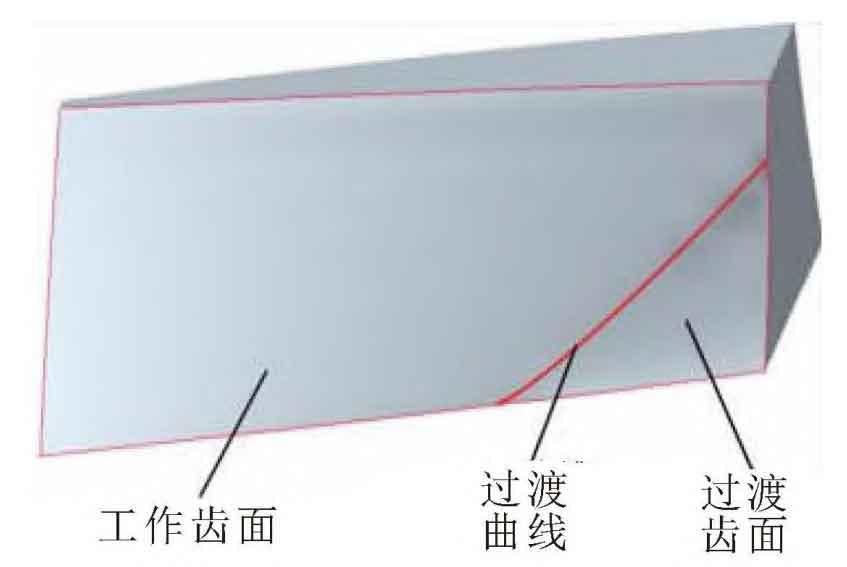
As shown in Figure 1, the tooth surface of the helical gear is composed of the working tooth surface and the transition surface. The working tooth surface is the two-degree-of-freedom envelope surface of the cutting edge space of the gear turning tool, and the transition tooth surface is cut from the tooth crest line of the gear turning tool. Obtain the tooth width of the helical gear, namely the minimum internal radius R1 without undercutting and the maximum external radius R2 of the constant tip of the tooth top.
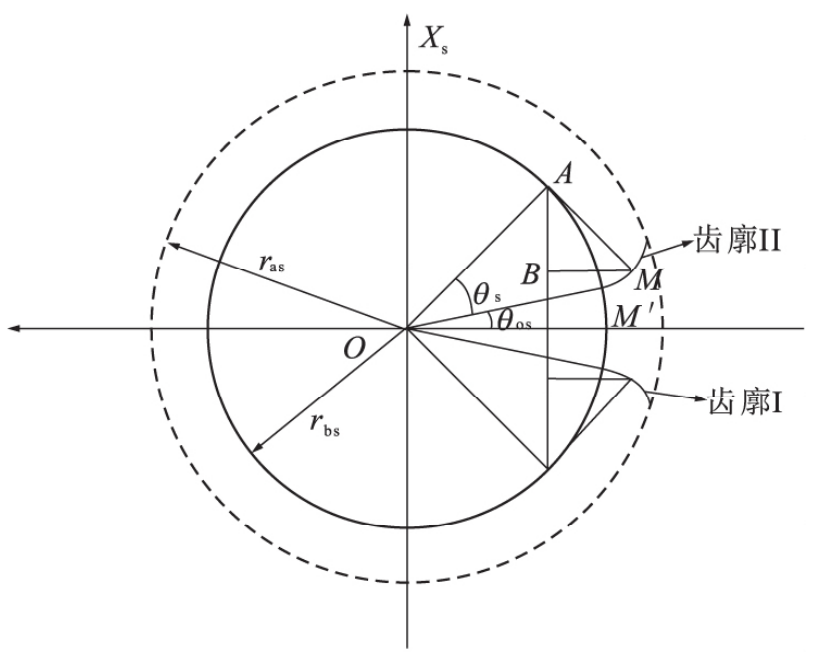
During virtual gear shaping of helical gear, the direction of tool feed is perpendicular to its normal surface, that is, the normal tooth profile of gear shaping cutter (generating gear) envelops the tooth profile of face gear. Therefore, taking the imaginary normal section tooth profile of the generating wheel as the cutting edge curve of the turning tool, and taking the imaginary equivalent gear tooth number of the generating wheel as the number of teeth of the turning tool, through the two-degree-of-freedom turning action of the tool and the workpiece, the high-precision helical gear tooth surface can be obtained theoretically. The research shows that the normal tooth profile of helical cylindrical gear is similar to the involute tooth profile, so the involute tooth profile is taken as the edge profile curve of gear turning tool in this paper (see Figure 2), and its equation is:
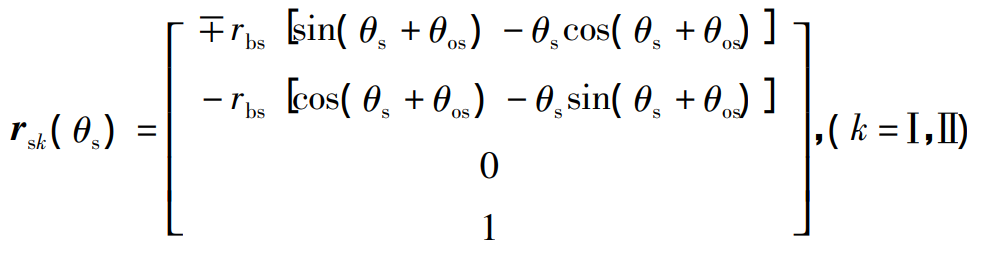
Where, rbs is the base circle radius of the gear turning tool; θ S is the angle parameter of any point on the involute of the gear turning tool; θ Os is the angle between the symmetrical line of the tooth slot of the turning tool and the involute of the tool at the starting point of the base circle, and its size is:
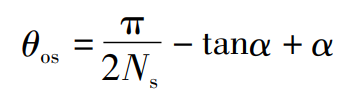
Where, Ns is the number of teeth of the gear turning tool; α Is the pressure angle of the involute of the gear turning tool.
