Calculation of contact line length of helical gear
The length of contact line of helical gear has a great influence on the load distribution of helical gear teeth. The contact line length of helical gear is related to its total contact degree.

It can be seen from the previous research that the total coincidence degree of helical gears is divided into end face coincidence degree and axial surface coincidence degree. According to the size of end face coincidence degree and axial surface coincidence degree, helical gears can be divided into two types: the first type is that the end face coincidence degree of the gear is greater than its axial surface re combination degree, that is, ε α > ε β; the second type is that the end face coincidence degree of the gear is less than its axial surface coincidence degree, that is, ε α < ε β εβ。 For helical gears, the total contact degree of helical gears has a certain relationship with the contact line length: the greater the total coincidence degree of helical gears, the larger the contact line length, the smaller the unit contact line load, and the greater the contact fatigue strength. As shown in the figure, the effective contact width be is calculated according to the contact line of the two kinds of gears mentioned above.
The first kind of helical gear (ε α > ε β)
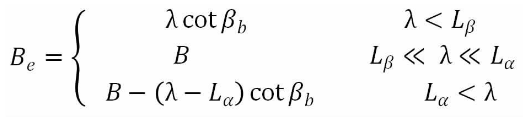
The second type of helical gear (ε α < ε β)
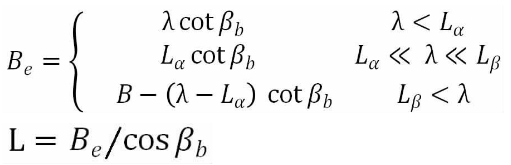
Calculation of unit contact line load of helical gear
In the process of actual meshing, the meshing line of helical gear changes from point to line and then to point. Therefore, in order to obtain the normal contact load distribution of helical gear at different meshing positions, considering the actual situation, the unit normal load of contact line can be obtained by dividing the total normal load by the length of the total meshing line.
It can be seen from the previous research that the total coincidence degree of helical gear represents the number of teeth engaged in the meshing process. After getting the contact line length variation diagram of a single tooth, the second pair of teeth is one cycle longer than the first pair of teeth, the third pair of teeth is one cycle later than the second pair, and so on, the total contact line length lt can be obtained.
The total normal load is as follows:
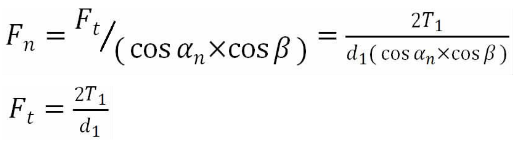
Where:
FT — axial force, N;
T1 — torque, n · M.
Unit contact line load:
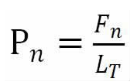
When the total contact degree of helical gear is larger, the contact line length of helical gear is longer, the unit contact line load is smaller, the bearing capacity is stronger and the transmission is more stable.
