The dual input single output helical gear transmission system under asymmetric loads has become an important structure in the power propulsion equipment of large ships due to its advantages such as high power density, compact structure, and flexible power parameter ratio. However, due to the particularity of the structure, with the increase of power, the helical gear at the low load end undergoes a transition from passive power consumption to active power, which means that the connected helical gear pair switches from back meshing to forward meshing, and nonlinear instability phenomena such as tooth collision, vibration, and noise occur, thereby affecting the safe and stable operation of the propulsion system. Therefore, considering various nonlinear factors that affect the operational stability of the system, establishing a typical dynamic model of a dual input single output helical gear transmission system, and studying the influence of asymmetric dynamic parameters on the vibration characteristics of the system are the key to scientifically explaining the instability mechanism and suppressing the occurrence of instability phenomena.
There have been many research achievements in modeling the dynamics of helical gear systems. According to the different degrees of freedom of the system, there have been models such as pure torsion model, bending torsion coupling model, bending torsion pendulum coupling model, and bending torsion pendulum axis coupling model. In the 1980s, Iida et al. established a bending torsion coupling model for a helical gear system and studied the dynamic characteristics of gear meshing; Kahraman comprehensively considered the translation and oscillation characteristics of the gear rotor system in two orthogonal directions in a plane perpendicular to the shaft, and established a coupled vibration model of the gear rotor system with bending torsion pendulum; With the deepening of research on coupling systems, Eritenel et al. established gear bending torsion shaft pendulum coupling models and conducted finite element analysis and experimental method research on dynamic characteristics. The internal excitation generated by the tooth meshing itself and the external excitation caused by other factors in the system are key factors that affect the stability of the system operation.
Feng et al. derived a calculation method for the time-varying meshing stiffness of helical gears through the slicing method, and compared the calculation results with the finite element method; Guilbault et al. studied the nonlinear meshing damping of single degree of freedom spur cylindrical gears and provided an empirical formula calculation method; Liu Zhansheng et al. further considered the influence of elastic shaft and unbalanced mass, established a dynamic model of gear rotor coupling system, and conducted experimental research; Ristivojevi ć A model based on the minimum elastic potential energy for non-uniform distribution of load along the contact line was proposed, and a formula for calculating the time-varying load distribution coefficient along the action line was derived; Gao established a dynamic model of a dual spur gear parallel drive system considering the stiffness of the oil film support, and studied the influence of the phase difference of the meshing stiffness of the two drive gears on vibration. There are also many in-depth research results on the evolution of the dynamic characteristics of gear systems with internal parameters.
Yang Shaopu et al. used the incremental harmonic balance method to study the nonlinear dynamics of spur gear systems and obtained the influence of system parameters on amplitude frequency characteristics; Cui Yahui et al. studied the influence of support stiffness and backlash on the vibration characteristics near the critical speed of the gear rotor system by analyzing the bifurcation characteristics under internal and external excitation; Li Yinong et al. considered the meshing force of gears, the meshing force of spline couplings, and the nonlinear contact force of bearings, and studied the influence of parameters such as meshing frequency, number of rollers, and bearing clearance on the vibration characteristics of the gear rotor bearing system.
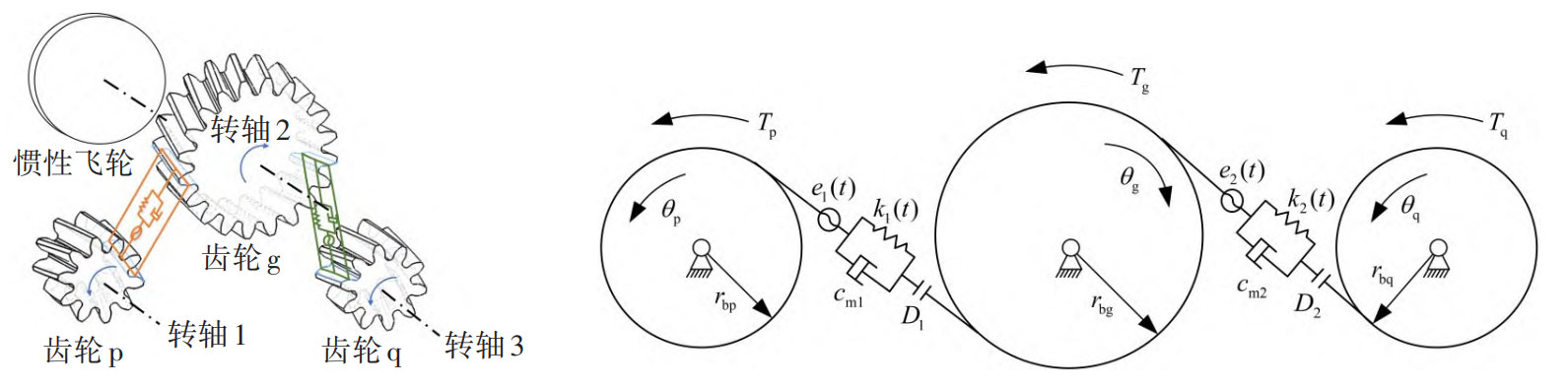
Although the dual input single output parallel helical gear structure is widely used in the power propulsion system of large ships, there is not much research on its dynamic characteristics, and the instability mechanism under asymmetric dynamic parameters is still unclear. On the basis of considering the time-varying meshing stiffness, meshing stiffness phase difference, nonlinear backlash, meshing damping, comprehensive meshing error and other parameters of helical gears, this article establishes a dynamic model of a dual input single output helical gear system, studies the evolution of the vibration characteristics of the system with asymmetric dynamic parameters, and elucidates the mechanism of system instability during operation.
