Abstract
Gear systems play a vital role in mechanical transmissions, and their reliability significantly impacts the overall performance of machinery. However, gear systems are prone to failures, with tooth root cracks being one of the most common issues. This paper focuses on analyzing the vibration response of gear systems containing tooth root cracks under both stable and variable load conditions. A modified potential energy method is proposed to accurately calculate the time-varying meshing stiffness (TVMS) influenced by crack parameters. Furthermore, a six-degree-of-freedom (6-DOF) dynamic model is developed to investigate the vibration response of cracked gear systems. The results demonstrate the influence of crack depth and angle on TVMS and the correlation between crack severity and vibration signatures.
1. Introduction
Gear systems are widely employed in various industries, including aerospace, automotive, and wind energy, owing to their high power transmission efficiency and reliability. However, these systems are prone to failure modes such as tooth root cracks, which can significantly affect their operational performance. The presence of cracks leads to a decrease in meshing stiffness, resulting in altered vibration signatures that can be leveraged for fault diagnosis.
1.1. Background and Motivation
Cracks typically initiate at the tooth root due to high stress concentrations and propagate towards the tooth tip or across the tooth width. This propagation affects the TVMS, which is a crucial internal excitation source for gear system dynamics. Accurate calculation of TVMS under cracked conditions is essential for precise dynamic modeling and reliable fault diagnosis.
1.2. Literature Review
Several studies have investigated the effects of cracks on gear dynamics. For instance, the potential energy method (PEM) has been widely used to calculate TVMS due to its computational efficiency [1]. Researchers have also explored vibration signatures of cracked gears through experimental and numerical methods [2, 3]. However, most studies focus on stable operating conditions, neglecting the impact of variable loads, which are prevalent in practical applications.
1.3. Objectives and Contributions
This paper aims to:
- Develop a modified PEM to accurately calculate TVMS considering crack depth and angle.
- Establish a 6-DOF dynamic model for cracked gear systems under both stable and variable load conditions.
- Analyze the vibration response of cracked gear systems and assess the sensitivity of various statistical indicators to crack severity.
2. Time-Varying Meshing Stiffness Calculation
2.1. Healthy Gear Meshing Stiffness
The PEM is based on the assumption that gears can be modeled as cantilevered beams with varying cross-sections. The TVMS is determined by considering the axial compression, bending, and shear deformation energies along with Hertzian contact stiffness. The total energy stored in the system can be expressed as:
U=Ua+Ub+Us+Uh
where Ua, Ub, Us, and Uh represent the axial compression, bending, shear deformation, and Hertzian contact energies, respectively.
2.2. Modified Potential Energy Method
To improve the accuracy of TVMS calculations, a modification to the standard PEM is proposed. The modification focuses on accurately capturing the deformation energies in the region between the base circle and the dedendum circle, which is typically neglected in conventional PEM. The modified bending, shear, and axial compression energies are given by:
Ub=21∫rbrfEI(x)M(x)2dx
Us=2G1∫rbrfκGA(x)(dxdu)2dx
Ua=2E1∫rbrfσ(x)ϵ(x)A(x)dx
where M(x) is the bending moment, κ is the shear correction factor, du/dx is the shear strain, σ(x) and ϵ(x) are the axial stress and strain, respectively, and EI(x), GA(x), and EA(x) are the bending, shear, and axial stiffnesses, respectively.
2.3. Cracked Gear Meshing Stiffness
For cracked gears, the presence of the crack reduces the effective cross-sectional area and moment of inertia, thereby affecting the deformation energies. The crack is modeled as a through crack extending symmetrically from the tooth root. Based on the crack depth and angle, four distinct models are developed to calculate the modified deformation energies.
Table 1. Crack Models Based on Depth and Angle
| Model | Crack Depth Condition | Inequality Constraints |
|---|---|---|
| 1 | q<0.5ha | ha≥h0 and a≤1 |
| 2 | q≥0.5ha or ha<h0 and a≤1 | |
| 3 | q>ha and hc<h0 | |
| 4 | q>ha and hc≥h0 |
3. Dynamic Modeling of Cracked Gear Systems
3.1. System Description
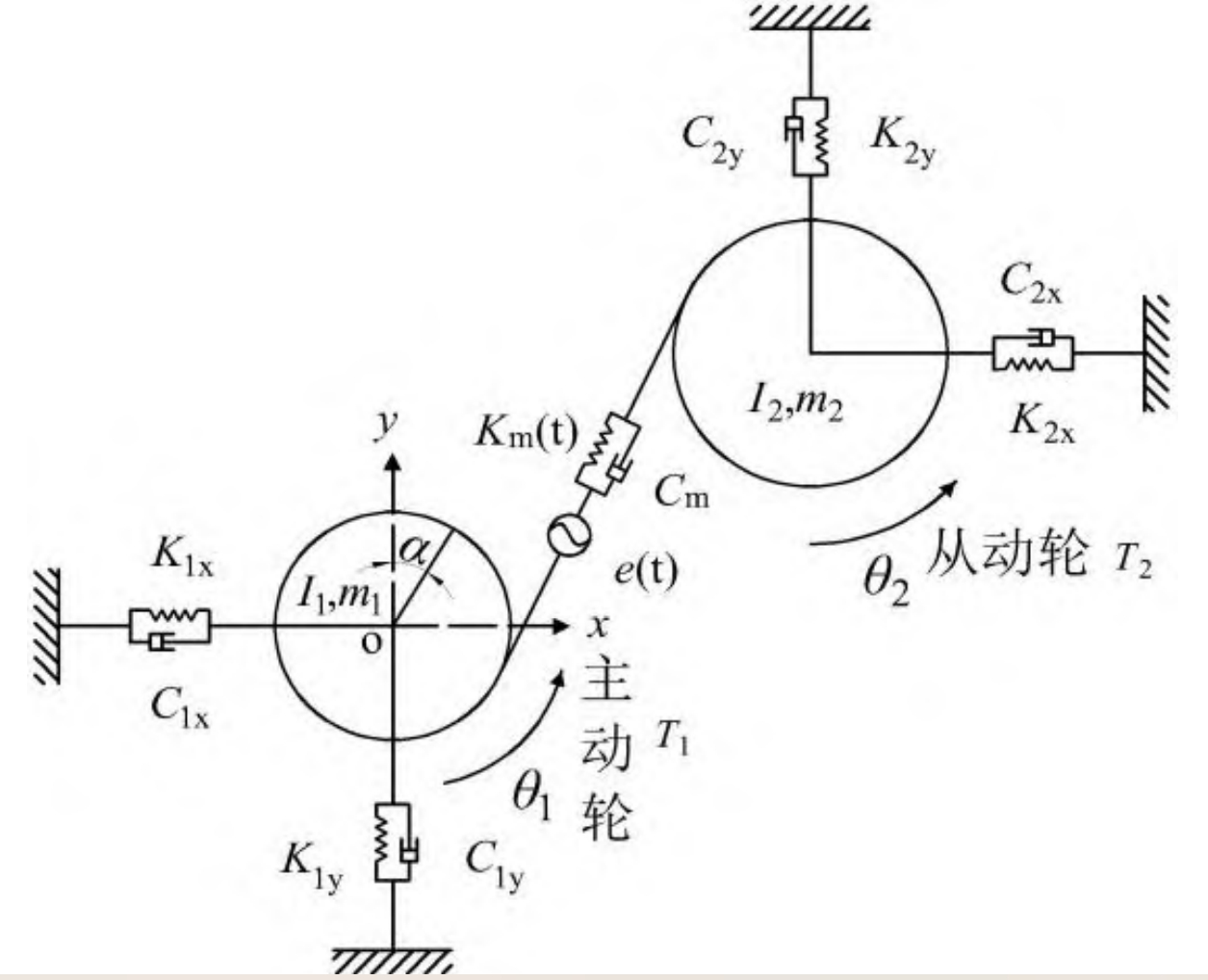
A 6-DOF dynamic model is developed for a cracked gear pair considering lateral, longitudinal, and torsional displacements. The model includes support stiffness and damping in both lateral directions, along with rotational inertia and meshing stiffness.
3.2. Equations of Motion
The equations of motion for the gear system can be derived using the Lagrangian approach:
(m1+m2)x¨p−m2x¨gcosα+m2θ˙g2rsinα+cp1(x˙p−e˙t)+kp1(xp−et)=0
(m2+J2θ¨g)r−m2x¨gsinα−m2θ˙gx˙grcosα+cp2(x˙g−e˙t)+kp2(xg−et)=T2
(m1+J1θ¨p)r+cm(x˙p−x˙g)+km(xp−xg)=−T1
where xp and xg are the lateral displacements, θp and θg are the angular displacements, cp1, cp2, and cm are the damping coefficients, kp1, kp2, and km are the stiffnesses, et is the transmission error, T1 and T2 are the driving and load torques, respectively, r is the base circle radius, and α is the pressure angle.
Table 2. Dynamic Model Parameters
| Parameter | Symbol | Value |
|---|---|---|
| Pinion mass | m1 | 0.32 kg |
| Gear mass | m2 | 1.3105 kg |
| Pinion inertia | J1 | 1.16×10−4 kg·m² |
| Gear inertia | J2 | 29.8 ×10−4 kg·m² |
| Pinion support damping | cp1 | 8 ×103 N·s/m |
| Gear support damping | cp2 | 8 ×103 N·s/m |
| Mesh damping | cm | Variable |
| Pinion support stiffness | kp1 | 1×109 N/m |
| Gear support stiffness | kp2 | 1×109 N/m |
| Mesh stiffness | km | Time-varying |
4. Vibration Response Analysis
4.1. Stable Operating Conditions
Under stable operating conditions, the vibration responses of both healthy and cracked gear systems are analyzed. The crack depth is varied from 0 to 2.94 mm (corresponding to 0%, 10%, 25%, 50%, and 70% of the tooth height).
4.2. Variable Load Conditions
The dynamic responses of cracked gears under variable load conditions are analyzed to mimic real-world operating scenarios. The load torque is varied sinusoidally with varying amplitudes.
5. Sensitivity Analysis
Statistical indicators, including root mean square (RMS), kurtosis, shape factor, crest factor, and peak factor, are utilized to assess the sensitivity of vibration signals to crack severity.
Table 3. Sensitivity of Statistical Indicators to Crack Severity
| Crack Depth (mm) | RMS (%) | Kurtosis (%) | Shape Factor (%) | Crest Factor (%) | Peak Factor (%) |
|---|---|---|---|---|---|
| 0.00 | 0 | 0 | 0 | 0 | 0 |
| 0.42 (10%) | 1.2 | 1.5 | 0.8 | 0.9 | 1.0 |
| 1.05 (25%) | 3.7 | 4.2 | 2.3 | 2.5 | 2.8 |
| 2.10 (50%) | 12.4 | 18.7 | 8.9 | 10.2 | 11.5 |
| 2.94 (70%) | 35.6 | 67.2 | 32.1 | 35.8 | 38.4 |
6. Discussion
The modified PEM accurately captures the effect of crack depth and angle on TVMS. The results indicate that crack depth has a more significant impact on TVMS than crack angle. The vibration responses under stable conditions reveal clear periodic impacts in the time domain and distinct sidebands around the meshing frequencies in the frequency domain. Under variable load conditions, the low-frequency components related to load fluctuations mask the crack-induced features, especially at higher load amplitudes.
Kurtosis emerges as the most sensitive indicator to crack severity, with a notable increase as cracks propagate. This sensitivity makes kurtosis a promising feature for crack detection and severity estimation.
7. Conclusion
This paper presents a comprehensive analysis of the vibration response of gear systems containing tooth root cracks. A modified PEM is developed to accurately calculate TVMS under cracked conditions. A 6-DOF dynamic model is established to investigate the vibration responses under both stable and variable load conditions. The results demonstrate the influence of crack depth and angle on TVMS and vibration signatures. Kurtosis is identified as the most sensitive statistical indicator for crack detection and severity estimation.
Future work could explore advanced signal processing techniques to enhance crack detection performance, particularly under complex operating conditions with high load fluctuations.
