In modern underground engineering, shield machines play an increasingly critical role, and the reducer, as a core component, directly influences the performance and safety of these machines. Among the reducer’s elements, multi-stage planet gears are vital, and their wear state significantly impacts the reducer’s efficiency and lifespan. Detecting the wear state of these planet gears is essential for ensuring the normal operation of shield machines and enhancing the safety and efficiency of underground construction projects. Traditional methods for monitoring planet gears wear, such as evaluating gear oil indicators or improved spectral residual-based techniques for spur gears, are often time-consuming and labor-intensive, making real-time detection challenging. To address these limitations, I propose a novel approach for real-time wear state detection of multi-stage planet gears in shield machine reducers, which improves operational safety and efficiency.
The detection method involves three main steps: vibration signal denoising for the reducer’s multi-stage planet gears, segmentation of the gear image meshing area, and detection of pitting regions. Each step is designed to handle the complexities of planet gears systems, ensuring accurate and efficient monitoring. Below, I detail the methodology, experimental setup, and results, incorporating formulas and tables to summarize key aspects.
Vibration Signal Denoising for Multi-Stage Planet Gears
Vibration signals from planet gears contain crucial information about their operational state, but they are often contaminated by environmental noise and electromagnetic interference, which affect signal stability and detection accuracy. To mitigate this, I employ a translation-invariant wavelet denoising method, which leverages wavelet transform properties for multi-scale analysis, separating noise from useful signals. This method enhances signal clarity and supports subsequent analysis.
The orthogonal wavelet transform decomposes a discrete signal into approximation and detail coefficients, facilitating noise reduction. Let the sampled discrete data be denoted as \( X_H \). The orthogonal wavelet decomposition of the planet gears vibration signal can be expressed as:
$$ X(t) = \sum_{j} d_j \cdot F_A \cdot n \cdot k $$
where \( d_j \) represents the scale coefficients, \( F_A \) denotes the wavelet coefficients, \( n \) is the number of filtering operations, and \( k \) is a constant. From a signal filtering perspective, orthogonal wavelet decomposition acts as an effective processing technique, where discrete signals pass through high-pass and low-pass filters to extract high-frequency and low-frequency information, respectively. This process filters out noise and preserves essential features.
The signal reconstruction process \( DFG \) is given by:
$$ DFG = x(t) \times \lambda $$
where \( \lambda \) indicates the number of wavelet decomposition layers. The denoising steps for the reducer’s multi-stage planet gears vibration signals are as follows:
- Input the collected planet gears vibration signal.
- Apply orthogonal wavelet transform to decompose the noisy signal into sub-signals, each associated with wavelet coefficients containing noise and signal characteristics.
- Perform multiple cyclic translations on the planet gears vibration signal using the formula:
$$ WG = A_v \times S_n \times \sigma_O \times DFG $$
where \( WG \) is the result of multiple cyclic translations, \( A_v \) is the translation cycle operator, \( S_n \) is the root mean square value, and \( \sigma_O \) is the soft threshold.
- Employ the soft threshold denoising method from the translation-invariant approach, defined by the soft threshold function:
$$ \sigma_O = \begin{cases} \text{sgn}(\sigma_O) \cdot (|\sigma_O| – T_\mu), & |\omega_{j,k}| \geq 1 \\ 0, & |\sigma_O| < 1 \end{cases} $$
where \( T_\mu \) represents the time-dimensional特征.
- Reverse the translation of the vibration signal and compute the average of the processed results.
- Output the denoised vibration signal for the reducer’s multi-stage planet gears.
This denoising process ensures that the signals are cleaner and more stable, which is crucial for accurate wear detection of planet gears.
Segmentation of Gear Image Meshing Area
Segmentation of the gear image meshing area is critical for identifying wear regions in planet gears. Traditional threshold methods often fail when gear regions are at the edges of grid areas, leading to incomplete segmentation. To overcome this, I use a combined approach of region segmentation, region aggregation, and edge correction. This method avoids detecting low-gray grid regions and handles variations in gear wear areas with different heights in images.
An adaptive local threshold is calculated to account for the varying gray features of planet gears wear parts, as global thresholding is unsuitable. The adaptive local threshold is defined as:
$$ Q_f = (A_1 \times A_2) \times SF \times \sigma_O $$
where \( A_1 \) and \( A_2 \) are the expectations of the source and target domains, respectively, and \( SF \) represents the特征 mapping in the planet gears space of the shield machine reducer. This threshold helps obtain candidate regions, and shape features are used to eliminate false positives.
To reduce segmentation errors, candidate grid regions are derived based on class grid region segmentation results. The correctness of the class grid segmentation is determined by the height of the segmentation result. Let \( Hei \) be the height of the grid segmentation region, and \( Thi \) be the coefficient threshold. The condition for incorrect segmentation is:
$$ Hei = Thi \times O_f $$
If this equation holds, the segmentation is deemed incorrect. The gear image meshing area is then obtained using:
$$ H(\omega, t) = Hei \times \eta \times \gamma $$
where \( \eta \) represents the time-frequency spectrum of the signal, and \( \gamma \) denotes the frequency-modulated signal. This calculation maps the depth features of vibration signals from the source and target domains into the planet gears space, minimizing the error between actual and expected classification results. The network parameters are fine-tuned based on this error, leading to accurate segmentation of the gear image meshing area for planet gears.
Detection of Pitting Regions
Pitting detection involves using adaptive local branch segmentation to identify candidate pitting regions, followed by the removal of pseudo-candidates using shape functions. Impulse excitation, a transient excitation method, is applied as it theoretically covers a continuous and constant frequency range, with energy concentrated in specific intervals. The modal test schematic for the planetary reducer box illustrates this process, which includes reading data streams, threshold processing, and detection.
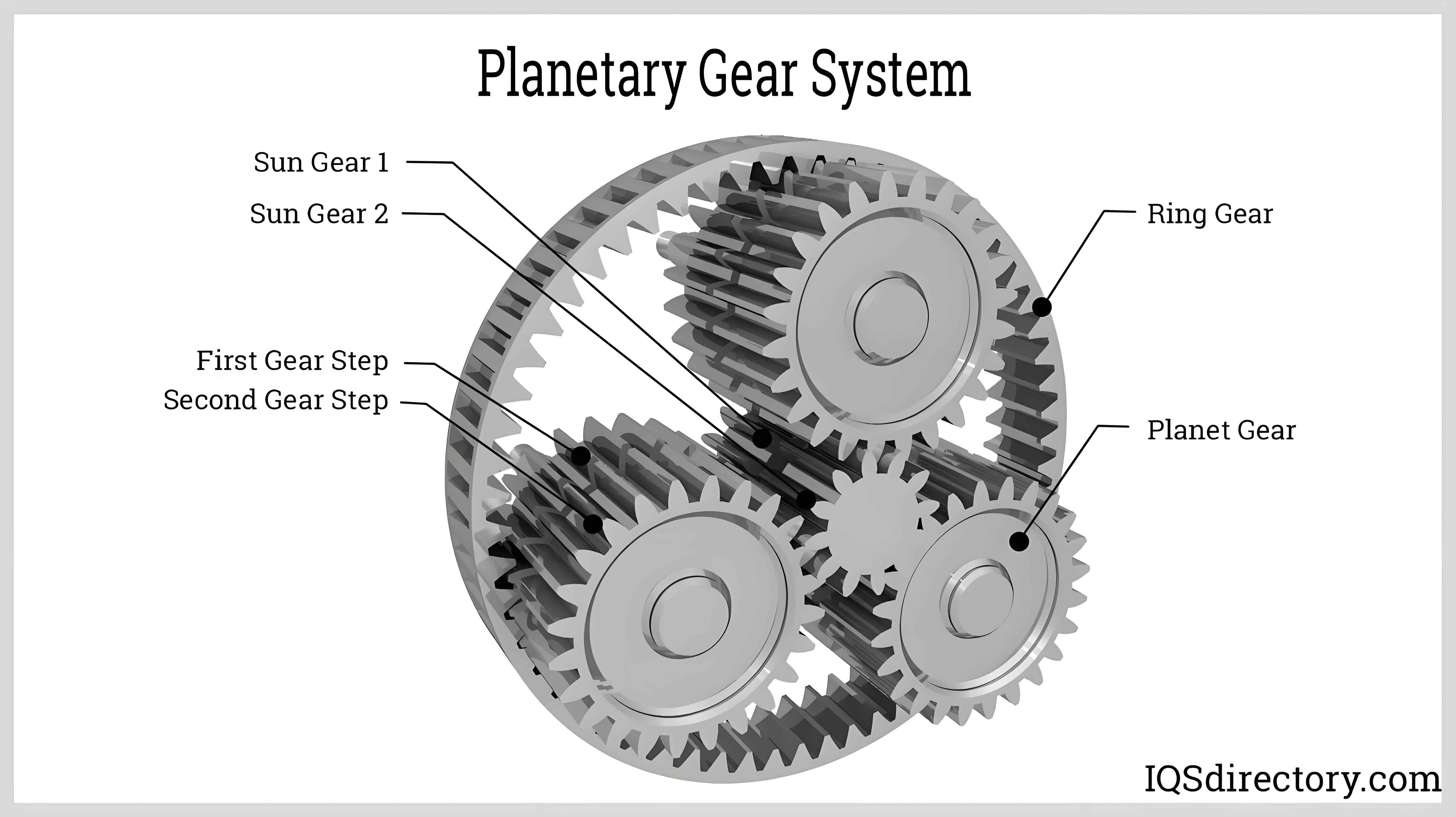
The main instruments and equipment used for detection are summarized in the table below:
| Name | Model | Performance |
|---|---|---|
| Computer | IBM | Standard computing capabilities |
| Multi-channel Data Acquisition System | LMS-SC305 | 16 channels |
| Data Analysis System | LMS Test.Lab Modal Analysis | Template-based analysis |
| Signal Conditioner | B&K Type 2692 | 4 channels |
| Acceleration Sensor | B&K 4326A-001 | Sensitivity 3 ±15% PC/g |
| Impulse Hammer | B&K 8202 | Sensitivity 3.97 pC/N |
To determine the main characteristics of the reducer box, free support boundary conditions are used in experiments, completing the detection process for planet gears.
Comparative Experiment
To evaluate the proposed method, I conducted a comparative experiment where my approach for detecting wear state in multi-stage planet gears of shield machine reducers was tested against two traditional methods: one based on monitoring fan gear oil indicators (Control Group A) and another using improved spectral residuals for spur gear wear detection (Control Group B). The experiment aimed to assess detection accuracy and efficiency.
The experimental setup involved signal acquisition using a multi-point excitation single-point pickup impulse excitation method. Key parameters for the planetary gearbox are provided in the table below:
| Parameter | Value |
|---|---|
| Module (mm) | 2.25 / 2.15 / 1.75 |
| Number of Teeth | 21 / 19 / 16 |
| Face Width (mm) | 13 / 14 / 16 |
| Addendum Coefficient | 1.0 |
| Dedendum Coefficient | 0.25 |
| Pressure Angle (°) | 20 |
| Gear Surface Processing Accuracy | Grade 8 |
The signal acquisition frequency was set to 11500 Hz, sampling time to 15 seconds, and the gearbox spindle speed to 19 r/min. This configuration ensured comprehensive data collection for analyzing planet gears wear.
The detection results were visualized through images of gear wear. The original gear wear image showed distinct wear patterns, while my method accurately identified all wear locations, matching the original. In contrast, Control Group A and Control Group B methods failed to detect all wear areas, indicating lower effectiveness. For instance, my method’s output closely aligned with the actual wear, whereas the control groups missed several critical regions.
To quantify performance, I tested the detection accuracy over 500 iterations. The results demonstrated that my method achieved an average detection accuracy of approximately 90%, significantly higher than Control Group A and Control Group B, which averaged around 70%. This highlights the superiority of my approach in accurately detecting wear states in planet gears.
The accuracy trends over iterations can be summarized as follows: my method consistently maintained high accuracy, while the control groups showed more variability and lower peaks. This reinforces the reliability of the proposed technique for real-time monitoring of planet gears in shield machine reducers.
Conclusion
The operational state of planet gears directly affects the performance of shield machine reducers, and regular detection of their wear state is essential for maintaining normal operation. The method I proposed for detecting wear in multi-stage planet gears significantly improves accuracy compared to traditional approaches. By integrating vibration signal denoising, adaptive segmentation, and pitting detection, this method provides a robust solution for real-time monitoring. Experimental results confirm its effectiveness, with minimal time deviations and high consistency with test data. This approach not only enhances the safety and efficiency of shield machines but also offers a reliable framework for future advancements in planet gears wear detection.
In summary, the use of translation-invariant wavelet denoising, combined with advanced segmentation and detection techniques, ensures precise identification of wear in planet gears. The comparative experiments validate the method’s superiority, making it a valuable tool for underground engineering applications. Future work could focus on optimizing computational efficiency and extending the method to other types of gears, further solidifying its applicability in industrial settings.
