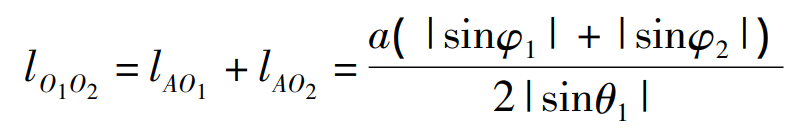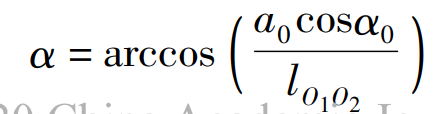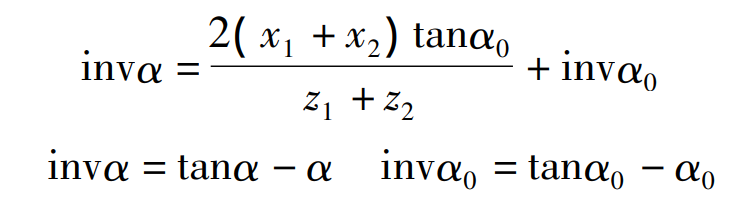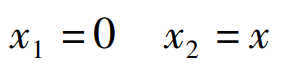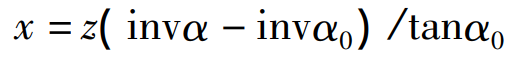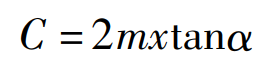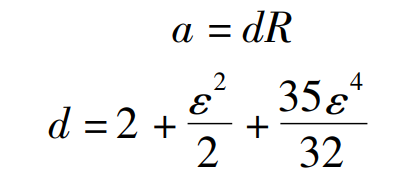The transmission between eccentric gears will produce backlash changes. Therefore, when calculating the displacement coefficient of eccentric modified gear in eccentric and eccentric modified gear transmission, we must first understand the variation law of backlash in eccentric gear transmission. When studying the seedling claw tip trajectory of the planetary system transplanting mechanism with eccentric displacement and eccentric gear transmission, using eccentric gear transmission instead of eccentric and eccentric gear transmission planetary system transplanting mechanism will simplify the analysis process and meet the requirements of seedling claw trajectory and angular displacement accuracy.
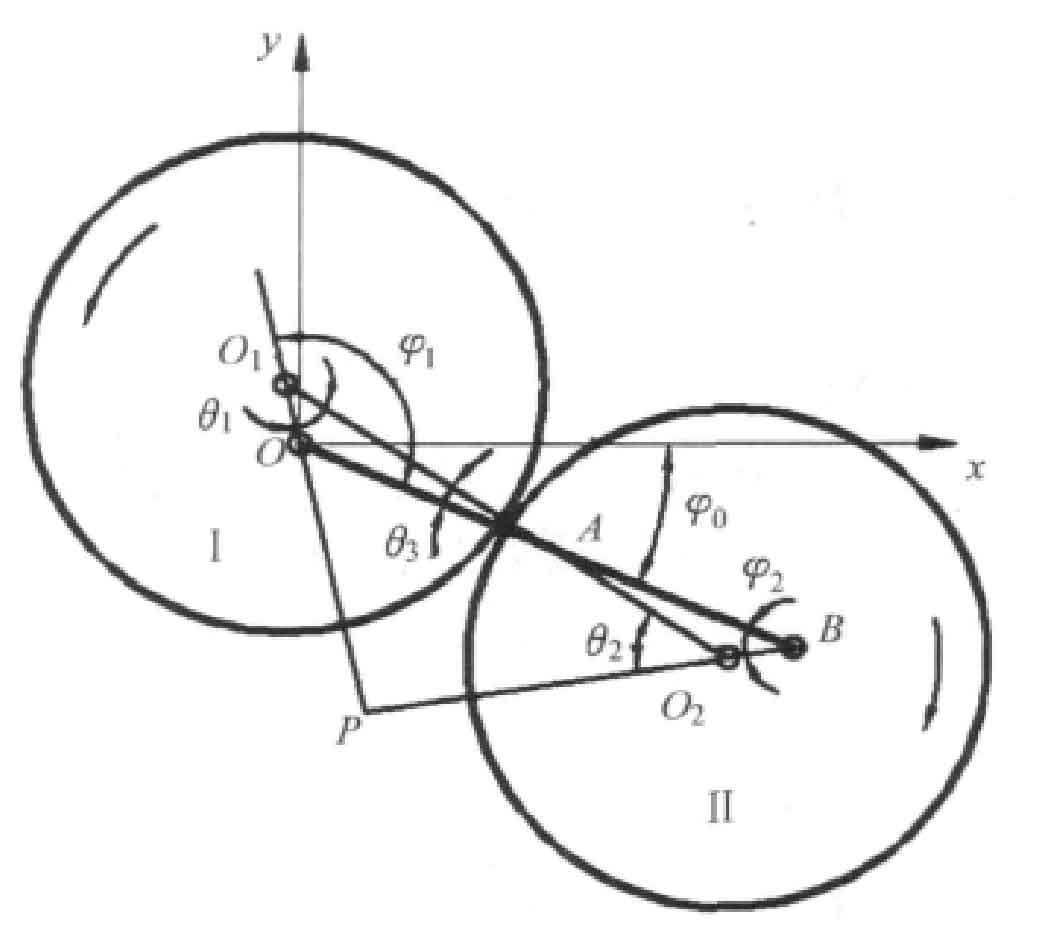
Two identical eccentric gears I and II mesh, as shown in Figure 1. In the initial position, the included angle between the axis OB and the x-axis is φ 0, oo1 coincides with OB, and Bo2 is on ob extension line. When gear I turns φ 1. Gear II φ 2. O1O2 and ob intersect at point a.
According to the transmission properties of eccentric gears, the geometric center distance at any position of eccentric gears I and II is:
Where: a — axial distance of two eccentric gears
According to the formula, in the process of eccentric gear pair transmission, the geometric center distance of the two gears changes with the angular displacement of the gear, so the tooth side clearance also changes.
At any time, the eccentric gear transmission can be regarded as the meshing of two standard cylindrical gears with center distance of lo1o2, and their rotation centers are O1 and O2 respectively, but the center distance of the two eccentric gears is no longer the standard center distance, but there is a side gap between the meshing tooth surfaces of the two eccentric gears.
The angular displacement of the gear is divided into N parts within the range of 0 ° ~ 360 °. Each point corresponds to a point on the pitch curve of the gear, and the angular displacement of the eccentric gear is carried out at each point, so as to change the tooth thickness of the gear teeth and make the tooth side clearance zero. According to the relationship between center distance and pressure angle, the actual pressure angle can be calculated:
Where: A0 — standard center distance, A0 = 2R
α 0 — standard gear pressure angle
Assuming that the tooth side clearance between two eccentric gears is C, in order to compensate the tooth side clearance, the eccentric gear is modified, and the eccentric gear transmission meets the meshing condition without tooth side clearance. The meshing equation without backlash is:
Where inv α = tan α - α inv α 0 = tan α 0 - α 0
Where: Z1, Z2 – number of teeth of eccentric gear I and II, and Z1 = Z2 = Z
X1, X2 — displacement coefficient of eccentric gear I and II
Since the eccentric gear is easy to process, the eccentric gear I is kept unchanged and only the eccentric gear II is displaced, that is:
The displacement coefficient of eccentric gear II is obtained as follows:
Thus, the tooth side clearance of the eccentric gear is:
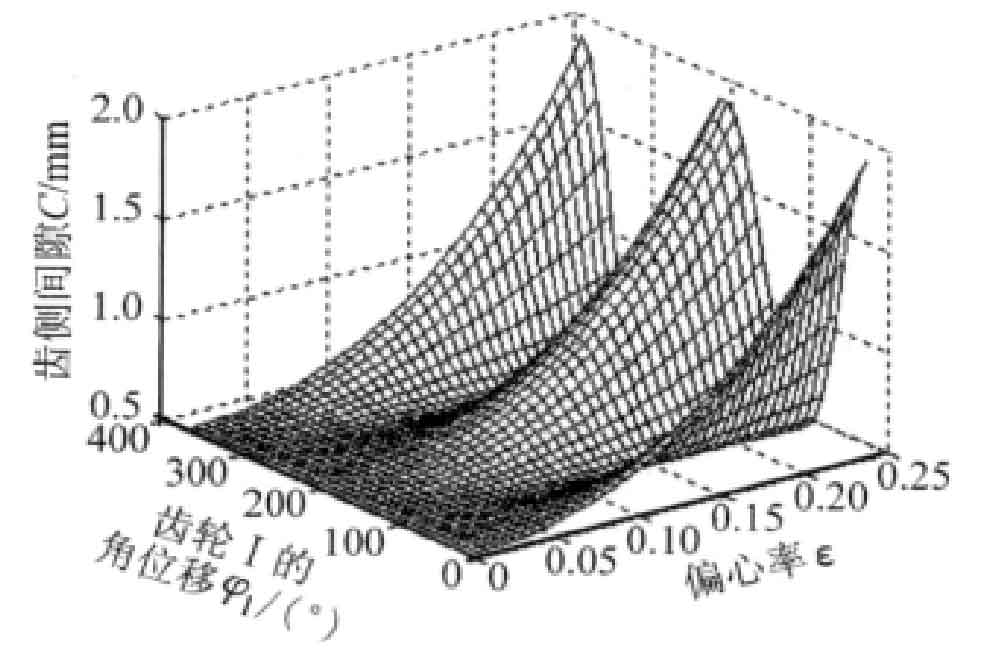
Figure 2 shows the clearance C and angular displacement between teeth φ 1 and eccentricity ε Relationship. It can be seen from the figure that the tooth side clearance changes periodically within one cycle of gear rotation. With the increase of eccentricity, the tooth side clearance increases, far exceeding the allowable range. If the gear is applied to the transplanting mechanism of the rice transplanter, the tooth side clearance will be transmitted to the seedling needle through the gear and the planting arm, resulting in the vibration of the transplanting mechanism and the swing of the seedling needle, which will lead to uneven seedling collection, or the seedling needle will not reach the seedling or collide with the seedling door.
In order to avoid reducing the coincidence degree due to excessive displacement coefficient, and to reduce the structural size, properly reduce the shaft center distance on the premise of meeting the gear strength and no undercutting. The axial distance between eccentric gear and eccentric displacement gear is:
Where D — relative center distance of two gears
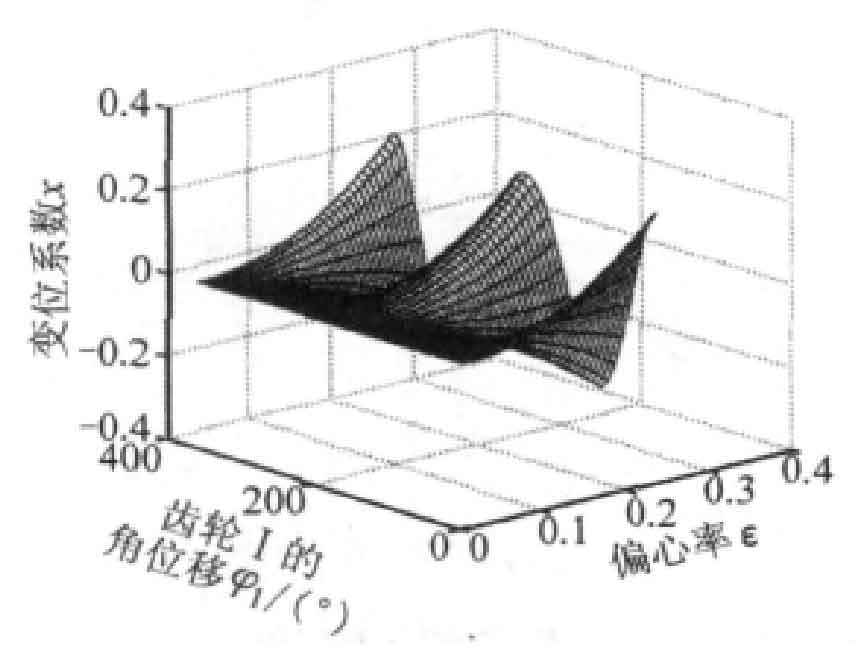
Figure 3 shows the displacement coefficient X and angular displacement φ 1 and eccentricity ε Relationship. It can be seen from the figure that the displacement coefficient is positive and negative. If the eccentricity is zero, the displacement coefficient is zero and no displacement is required. If the eccentricity is not zero, the displacement coefficient changes periodically and the gear rotates twice a week. The greater the eccentricity, the greater the fluctuation, and the fluctuation law is the same. The displacement coefficient is the largest at 0 ° and close to 180 ° and the smallest at slightly less than 90 ° and slightly greater than 270 °.