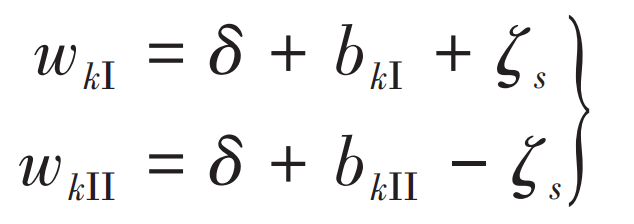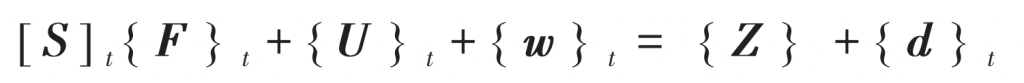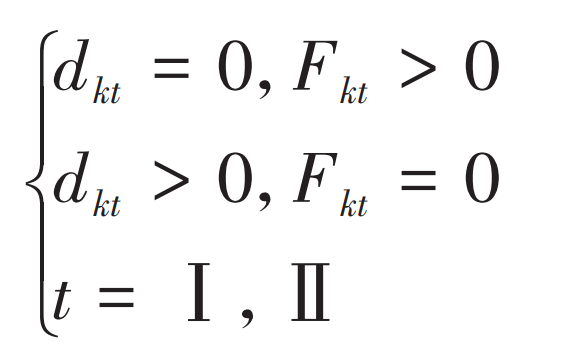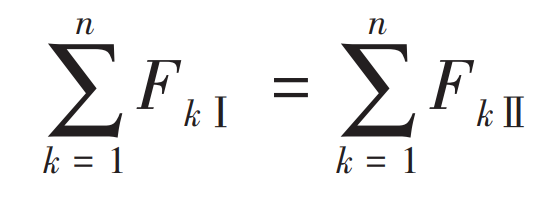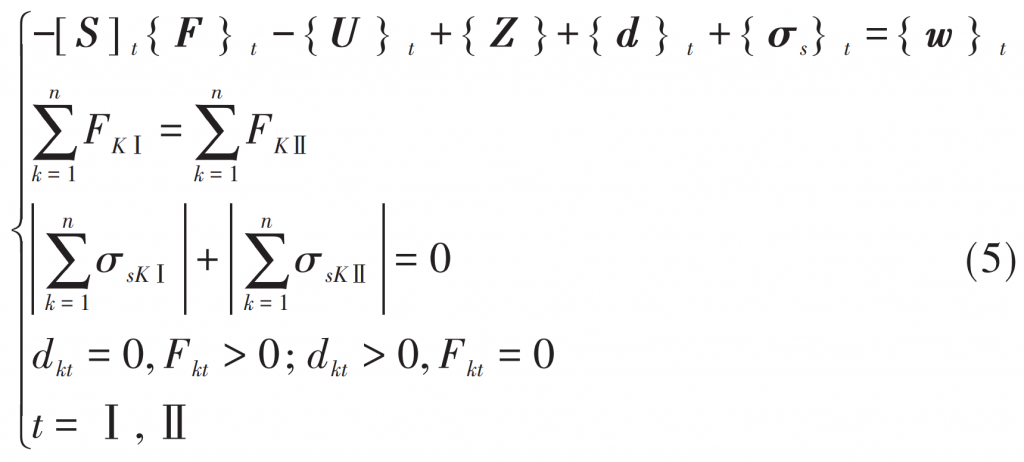Based on the helical gear LTCA model obtained by Litvin et al. Based on the finite element loading contact analysis principle, the herringbone gear loading analysis model is regarded as the parallel connection of the left and right helical gear contact models. According to the gear meshing theory and computer simulation technology, the loading contact of herringbone gear pair is simplified into the contact process of two elastomers.
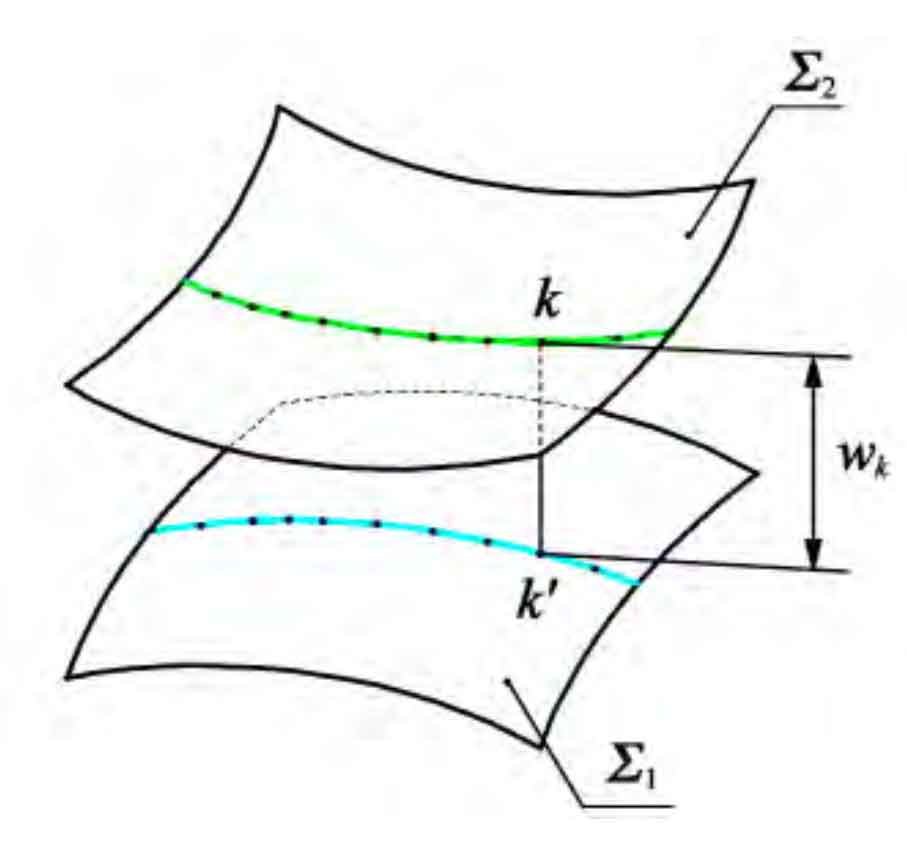
According to the relevant theory of helical gear, the tooth contact area is regarded as the line contact along the long axis of the tooth surface contact ellipse, and then the instantaneous contact of the gear pair meshing transmission is simplified as the contact of N discrete points on the two tooth surfaces along the long axis of the instantaneous contact ellipse, in which the initial clearance of the wheel teeth at any point K on the long axis of the ellipse before contact is recorded as wk, as shown in Fig. 1.
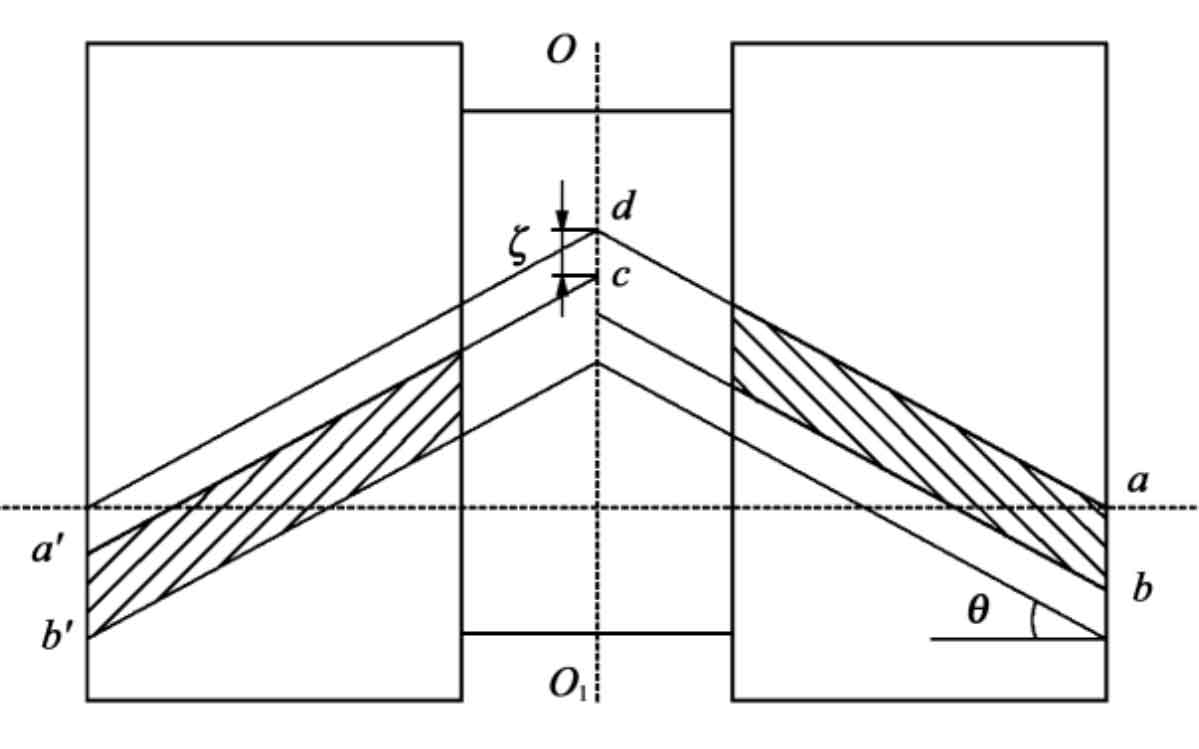
Without considering the manufacturing or installation errors, the axial forces generated can offset each other because the two helical gears constituting the herringbone gear are completely symmetrical. However, due to the influence of processing equipment and manual operation, the left and right helical gears of the actually processed herringbone gear will appear incomplete symmetry, as shown in Figure 2. When the tooth direction of the right helical gear is taken as the reference, the distance between the extension lines of the two tooth lines of the left and right helical gear teeth of the herringbone gear in the vertical direction O1O2 is recorded as the centering error ζ。
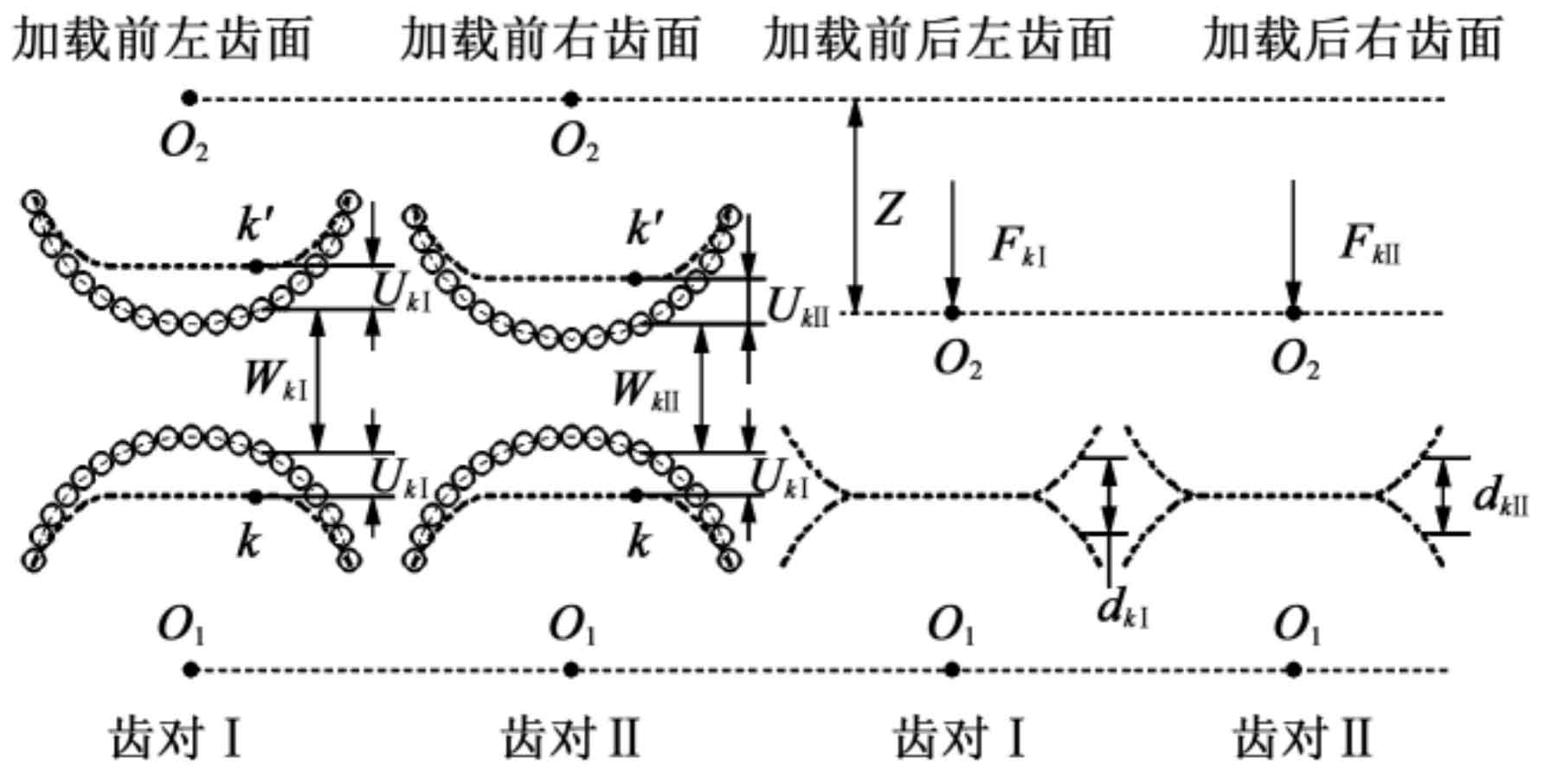
At a certain time, the left and right ends of herringbone gear pair are in contact with tooth pair I and tooth pair II, and the balance model of tooth loading displacement is shown in Fig. 3. Among them, the distance between discrete points K on the long axis of the instantaneous contact ellipse is recorded as BK, and the transmission error is recorded as δ, The upward half of the centering error in the meshing method is recorded as ζ s. Then the initial clearance of discrete point K before tooth deformation is:
The gear is elastically deformed under the action of external load P. it is assumed that the pinion is fixed and the large gear will produce normal displacement Z under the action of P. By expanding a single discrete contact point on the instantaneous contact ellipse of the tooth surface of two herringbone gear transmission to n points, the displacement coordination equation of standard herringbone gear transmission is:
Where, T represents tooth pair I and tooth pair II; [S] Is the tooth bending shear flexibility coefficient matrix; {F} Is the load vector of each discrete contact point; {U} Is the contact deformation vector of each discrete contact point; {w} Is the initial clearance vector at each discrete contact point before tooth loading deformation; {d} The residual clearance vector at each discrete contact point after tooth deformation is loaded.
In the process of contact transmission, the tooth surface will not be embedded, and the conditions to be met are:
Due to the alignment error of herringbone gear system, the initial clearance between the left and right tooth surfaces is different, resulting in different load on the two tooth surfaces during loading, resulting in large axial force. Usually, in order to eliminate the axial force, the herringbone gear system adopts the installation mode of small wheel axial floating through the axial movement of small wheel in the process of meshing transmission σ, Make the tooth surface clearance of tooth meshing consistent, so as to balance the axial force of left and right meshing tooth surfaces. Therefore, the force balance constraint equation is introduced as follows:
To sum up, according to the deformation coordination relationship before and after loading, the two-layer iterative method combined with the golden section method is used to solve the loading contact equation of herringbone gear teeth as follows:
Where{ σ s} When the position coordination equation is superimposed, the values of the left and right tooth surfaces are opposite.