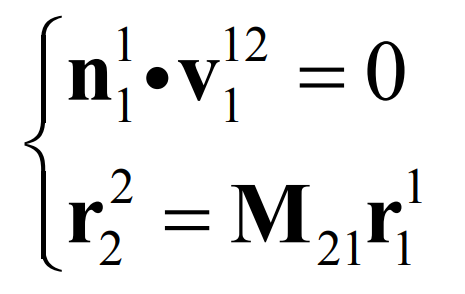The design theory and design method of pure rolling contact conjugate curve bevel gear have been discussed. However, in the current industry, the main gears used are non pure rolling contact gears, such as Gleason tooth circular arc tooth bevel gear, Klinger tooth and orikon tooth long external swing bevel gear. In fact, when there is a little installation error, the pure rolling contact bevel gear can easily become a non pure rolling contact state. Therefore, the conjugate curve bevel gear under general contact condition has greater universality. Therefore, in this chapter, the main properties of conjugate curve bevel gear under general contact conditions are studied. For conjugate curve bevel gear under general contact conditions, its contact line still needs to meet the general conditions of conjugate curve design theory. The conjugate curve equation is composed of formula:
The establishment of the meshing equation is mainly based on the pure rolling contact condition V12 ≡ 0. When V12 ≡ 0, N1 V12 = 0 exists for any vector N1 according to the vector calculation law. However, for general conjugate curve bevel gears, there is no condition of V12 ≡ 0. Therefore, in Chapter 3, the formula based on V12 ≡ 0 is not suitable for conjugate curve bevel gears with general contact conditions. In this chapter, the properties of conjugate curve bevel gears under general contact conditions will be discussed.