Introduction
Gear vibration and noise are important parameters that affect transmission performance,The vibration and noise control of gear transmission system has become a very importantResearch field.Consider the multi-degree-of-freedom coupling of gear shaftsand taking into account the effects of nonlinear backlash and time-varying meshing stiffness,The vibration characteristics of helical gear systems were studied.Linear dynamic model of gear pair, which considers the flexibility andThe floating of the bearing and the multi-degree of freedom due to gear meshingThe dynamic coupling between the motions is investigated, and the influence of the helix angle on the free and forced vibration characteristics of the gear pair is studied.Considering the time-varyingInfluence of meshing stiffnessIn the following, two coupling models (lateral-torsional coupling model and lateral-shear coupling model) are adoptedThe coupled model of axial-torsional-axial oscillation) is used to analyze the dynamic characteristics of the helical gear system.research on the meshing behavior of gear pairs is conducted.time-varying stiffness and viscous damping proportional to the meshing stiffness,A pair of low-contact-ratio spur gears with single degree of freedom model was used to study the spur gearsteady-state response and stability.Studied the non-equidistant toothwheel, and derived the non-uniform geometric equation of non-equidistant gears.Three-dimensional nonlinear vibration of gear pairs was studied.Numerical simulation technology was used to study the influence of involute coincidence degree, bearing support,Dynamic transmission error of helical gear system affected by bearing stiffness, meshing damping and backlashand vibration stability.For rings with multiple planetary wheelsThe research on the shape gear ring shows that under certain conditions,The phase difference between the two channels can eliminate large amplitude response.A method is proposed toApplicable to the process of variable speed (including acceleration, deceleration, and large speed fluctuation processetc.), and presents a planetary gear set modelSuggestions on avoiding tooth separation and tooth back contact in the design and suppressing vibration.
At present, the main methods of vibration control for gear transmission systems include increasingTo increase the degree of engagement, shape modification, displacement, damping, etc. The meshing phase of the gear train isan important parameter for studying the vibration performance of gear transmission.In recent years,Many scholars have conducted extensive research on meshing phase.Through the study of meshing force, a rigorous analysis of the phenomenon of phase tuning was conducted.Mathematical derivation and analysis of the transmission ratio of planetary gears through meshingDesign principles for certain harmonics of phase-suppressed planetary modal response;Zhang JiaXiong et al. studied the parameter design and dynamic response of high-order tuned gears,Derive the optimal transmission parameters of the tuned gear, verify the correctness of the tuned gearThe influence of time phase angle and tuning order on dynamic response.This paper studiesThe principle of gear meshing with misaligned tooth phase tuning is derived, and theCalculation formula for time-varying meshing stiffness of harmonic gears, and study of misalignment phaseThe mapping relationship between tuning and vibration response is the key to the optimization of the gear transmission system.The vibration control of the system provides a new idea.
1. Principle of wrong tooth phase tuning
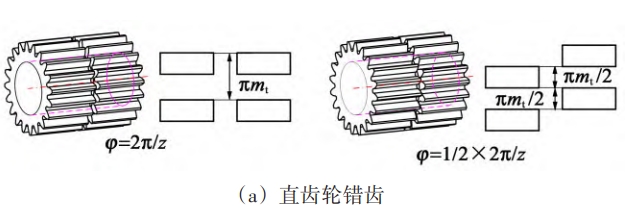
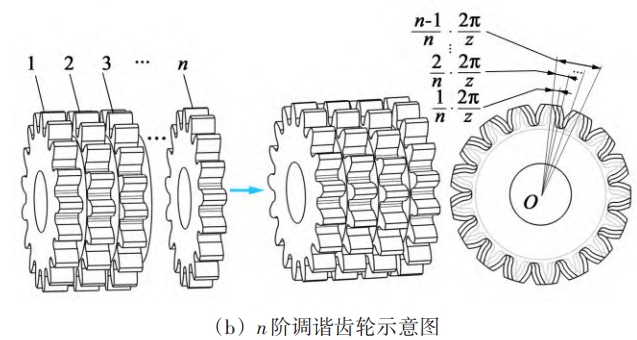
For a spur gear with a tooth width of b, it can be divided into two parts with a tooth width ofb/n spur gears, and note down these two gears with a tooth width of b/nFor the first, second, third, … and nth layers, and the distance between two layersBy staggering the angle, it is possible to make a single pair of such gears existThe gear phase difference is engaged, and this change does not affect the gear ratio, satisfyingThe principle of gear meshing at each level, so that it can be adjusted by adjusting the meshing phaseThis method is called misalignment phase in this article.The corresponding gear is called the misaligned phase tuning gear, which is used for tuning method.The angle of the angle should be called the misalignment phase angle, as shown in Figure 1.
For a parallel shaft single-stage transmission system comprising two meshing pairs,Suppose that the gear on one side remains unchanged, and the gear on the other side rotates along the circumference.Turn to a certain angle.When it turns through 1 standard tooth slot width πmt/2When , the corresponding pitch angle is π/z, at this time, the tooth groove of a gear corresponds toThe corresponding meshing stiffness function curve and label of the gear tooth of the other gearThe difference between the quasi-engagement stiffness function curves is half of the engagement period Tm/2;when the rotation angleTurn 1 standard pitch πmtThe corresponding pitch angle is 2π/z. At this time,Corresponding meshing stiffness function curve and standard meshing stiffness function curveThe difference is 1 meshing cycle Tm, due to the periodicity of the meshing stiffness function.The two function curves are completely coincident.
For a parallel shaft single-stage transmission system with two meshing pairs,The relationship between the misalignment phase p and the misalignment phase angle φ is

Where, z is the number of teeth of the driving gear.Due to the periodicity of gear meshing,The misalignment phase angle cannot exceed 1 standard pitch angle 2π/z, which is the maximum misalignment angle.The relationship between the position angle φ and the angle φ0 that one side of the gear rotates is

In the formula, mod() is the remainder function.
Principle of wrong tooth phase tuned gear transmission
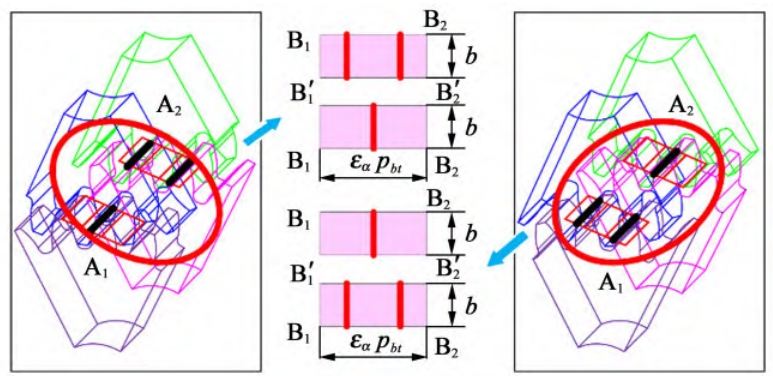
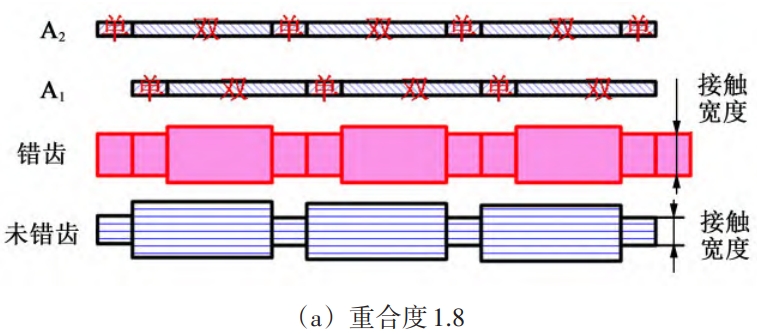
Due to the fact that the adjacent two gears are offset by a certain angle in the circumferential direction,Therefore, the corresponding gear teeth on the two meshing gear pairs will not enter the real space at the same time.This results in two meshing gear pairs at the same timeThe position of the multi-tooth meshing area and the low-tooth meshing area are not the same.For standard spur gears, the degree of coincidence is 1 < ε < 2, and the meshingThe process always exhibits periodicity between single-tooth meshing and double-tooth meshingFor tuned spur gears, two meshing gear pairs rotate along a circleThe direction of the circumference is staggered by a certain angle, and the gear teeth in the two meshing gear pairsThe time to enter the actual meshing area is not consistent.Therefore, in a meshingWhen the gear pair is in the single tooth meshing area, by adjusting the phase angle of the misalignment,This may cause another meshing pinion to be in the double-tooth meshing area, and vice versaSimilarly, two meshing pairs with wrong tooth phase can be understood asTwo meshing pairs with different initial meshing phases are involved, as shown in Figure 2.For standard spur gears, the two meshing pairs always enter the singleThe tooth meshing area or the double tooth meshing area is simultaneously entered, with one side of the tooth set hereThe width of the wheel is b, then the total length of the contact line of the standard spur gear meshing pair isfluctuates between 2b and 4b.For misaligned phase-tuned spur gearsWhen the meshing pair A1 is in the single tooth meshing area, the phase difference can be adjusted by adjusting the misalignment angle.In the case of a 180° angle, the meshing pair A2 may be located in the single tooth meshing area, or it may be located in the double tooth meshing area.In the double-tooth meshing area, if the meshing pair A2 is in the single-tooth meshing area, then for the entire transmission pair, there are two pairs of gears engaged.The length of the integrated contact wire is 2b;if the meshing pair A2 is in the double-tooth meshing area,Then, there are 3 pairs of gears engaged in the entire gear pair, with a total contact line length ofdegree is 3b;similarly, if the meshing pair A1 is in the double-tooth region, the meshing pairA2 may be located in the single tooth meshing area (the length of the comprehensive contact line is 3b), orIt may be located in the double-tooth meshing area (the length of the comprehensive contact line is 4b), then theFor the entire misaligned phase-tuning gear meshing pair, this is also the optimal time.There are rarely 3 pairs of gears engaged.Figure 3 shows two different degrees of coincidenceThe schematic diagram of the contact line length change of the tuned spur gear pair.
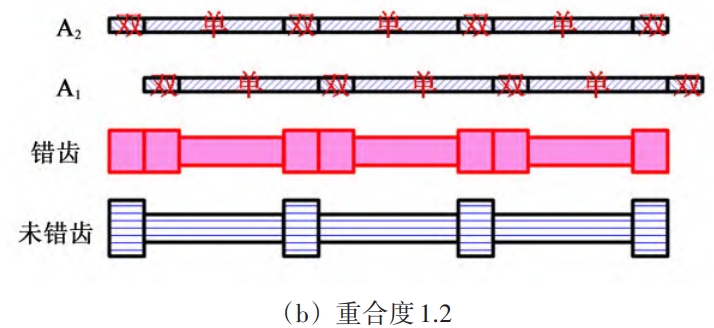
meshing stiffness of misaligned phase-tuning gear
To simplify the derivation of the formula, the meshing stiffness function is defined as the averageThe sum of the value and the change, that is,

In the formula, k- is the average value of the meshing stiffness over one cycle;Δk(t) isThe change in the meshing stiffness is partially periodic over time.For the misaligned phase-tuned gear pair, assume that two adjacent teethThe meshing stiffness of the wheel set is k(1( ) t), k(2( ) t), superscript (1) and subscriptThe symbol (2) is used to represent two gear pairs and define the initialThe initial meshing phase is p(1), p(2)Therefore, considering the wrong tooth phaseThe meshing stiffness of the two gear pairs is
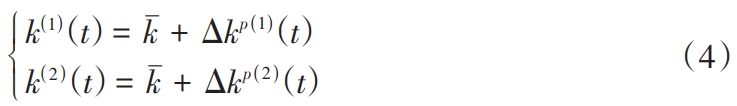
In the formula, kThe meshing stiffness of the single-side meshing pair is within 1 meshing cycle.The average value of Δkp(1)Δkp (2)The meshing stiffness of two meshing pairs isThe change in the degree is obviously Δkp(1)≠Δkp (2)。The wrong tooth phase tuning gear can be seen as two gear pairsAt the same time, it also participates in the meshing.Therefore, the single-sidedThe meshing stiffness of the meshing pair can be calculated by multiplying the meshing stiffness of the two meshing pairsWe can obtain it by averaging.Therefore, consider the misalignment phase tuningAfter that, the meshing stiffness of each gear pair is
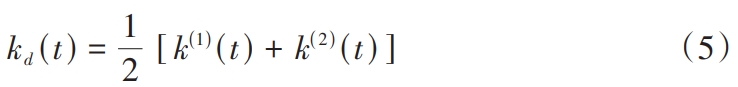
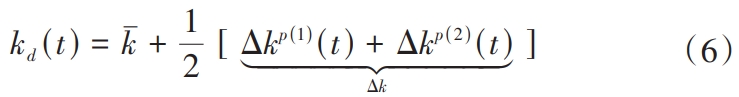
In the formula, k- the average value of the meshing stiffness of the gear pair tuned for misalignment phaseΔk is the change in the meshing stiffness of the misaligned phase-tuned gear,By further derivation of Fourier series expansion, we have
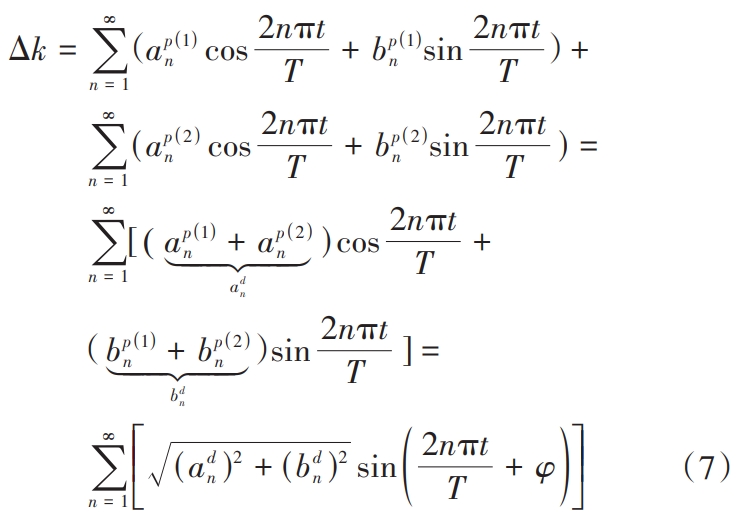
It can be found that the change of meshing stiffness of the misaligned phase-tuning gear isThe amplitude J of the part is related to α1, α2, α3, and p, that is, the phase modulation of the misalignment.The amplitude of the meshing stiffness of the harmonic gear is not only related to the misalignment phase, but also toThe original gear coincidence degree is relevant.For example, the coincidence degree ε0=1. If ε0 – 1 = 0.692 4 ≈ 2/3, then 3-order tuning is takenWhen n=1, the fluctuation of the meshing stiffness is the smallest.According to equation (13), n (n=1, 2,3) The amplitude components of the first 18 meshing stiffnesses of the tuned gear are added to obtainThe amplitude of the stiffness for different tuning orders is shown in Figure 4.
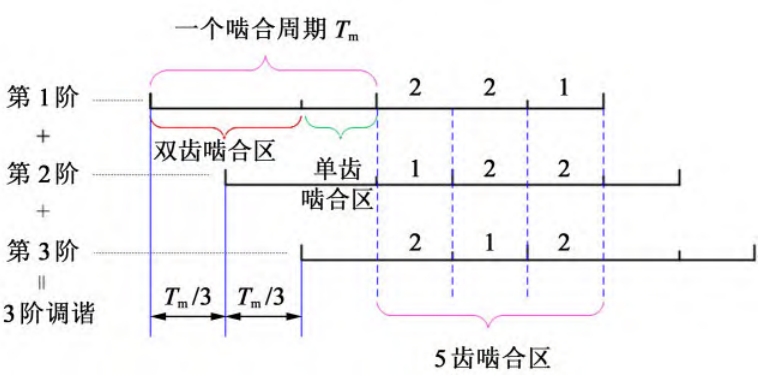
As shown in Figure 4, compared with traditional spur gears, the meshing of tuned gearsThe amplitude of the stiffness has decreased, among which the amplitude of the meshing stiffness during the 3rd order tuningThe reason for this phenomenon is that the complete meshing cycle of the spur gearThe period is the double-tooth meshing area plus the single-tooth meshing area.Single and double tooth meshing areaThe length of is directly affected by the degree of coincidence. When the degree of coincidence is proportional to c/3When c is an integer, the single and double tooth meshing areas are just in a multiple relationship, and the basic weightThe proportion coefficient of fit is about 2/3, that is, the double-tooth meshing area is close to the single-tooth meshingTherefore, one meshing cycle can be divided into three equalThe time zone is shown in Figure 5.
Conclusion
The meshing of the misaligned phase-tuned spur gear pair/helical gear pair was studiedThe relationship between stiffness and misalignment phase, and the effect of misalignment phase method on parallel stagesThe vibration reduction effect of the spur gear/helical gear transmission system;designed to achieveDevelop parallel shaft spur gear pair and helical gear pair with different misalignment phaseParallel axis spur gear pair and helical gear under different misalignment conditionsExperimental research on the secondary vibration response was conducted and compared with the simulation results.
