Abstract: This article focuses on the optimization design of hypoid gear using the multi-objective genetic algorithm. Hypoid gear is widely used in various mechanical transmissions due to their unique characteristics. However, traditional design methods often face challenges in achieving the best performance in terms of volume and noise. By establishing a mathematical model with the goals of minimizing the volume of hypoid gear pair and reducing noise, and applying the NSGA-II algorithm, significant improvements have been achieved in the design. The optimization process, results, and the practical significance of this approach are detailed in the following sections, providing valuable insights for the design and improvement of hypoid gear.
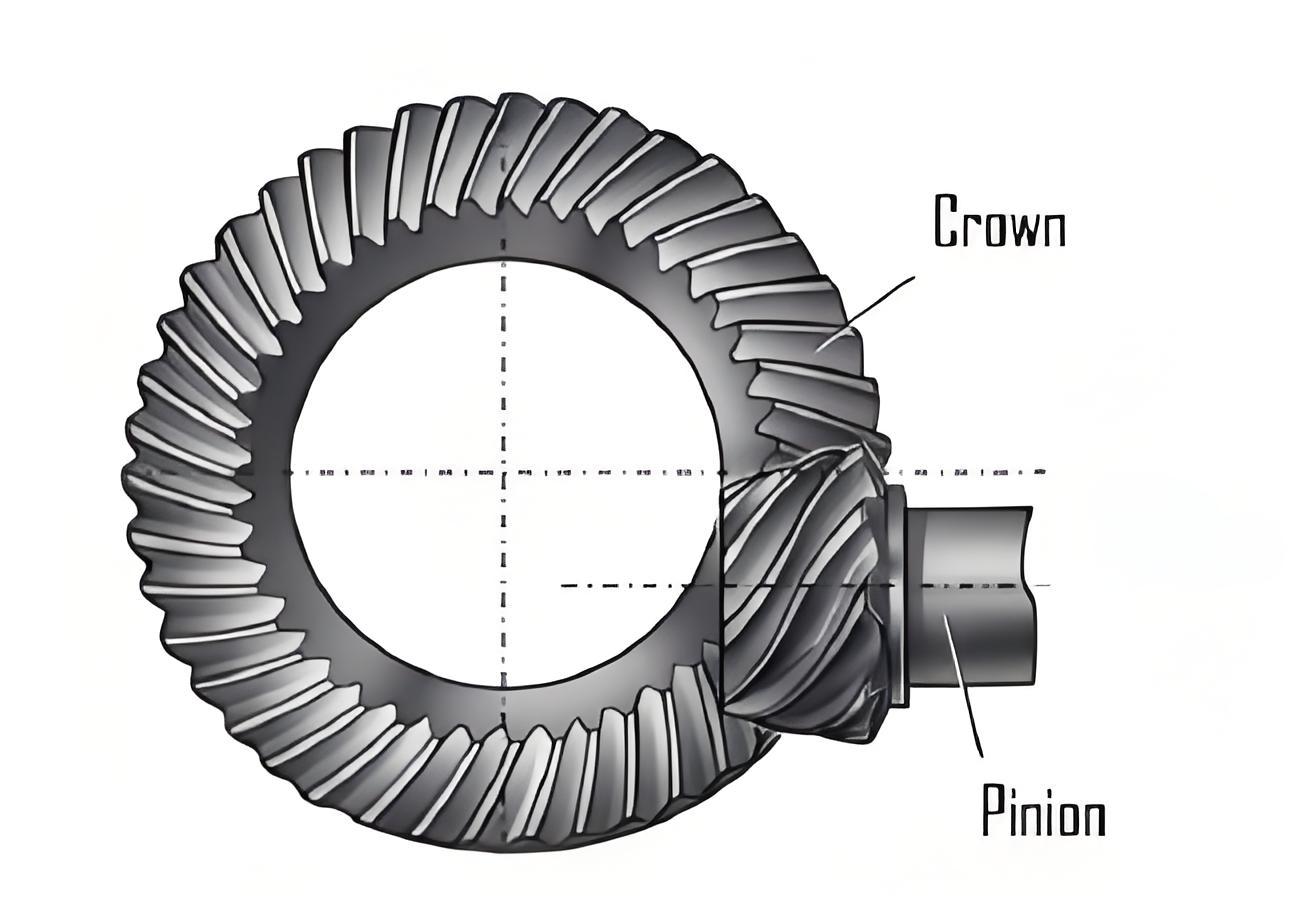
1. Introduction
1.1 The Importance of Hypoid Gear Optimization
Hypoid gear play a crucial role in mechanical transmissions, especially in automotive applications. Their ability to handle high speeds, high loads, and provide precise power transmission makes them an essential component. However, the design of hypoid gear is complex, and optimizing their performance is of great significance. For example, in automotive differentials, the performance of hypoid gear directly affects the vehicle’s handling, fuel efficiency, and noise levels. Minimizing the volume of hypoid gear pair can lead to lighter and more compact designs, reducing the overall weight of the vehicle and improving fuel economy. At the same time, reducing noise is essential for enhancing the driving comfort of passengers.
1.2 Challenges in Traditional Hypoid Gear Design
Traditional hypoid gear design often relies on empirical methods. Designers select gear parameters based on past experience and standard design guidelines. While this approach can produce functional gears, it may not result in the most optimal design. For instance, determining the number of teeth, the diameter of hypoid gear, and other parameters solely by experience may lead to suboptimal gear pairs in terms of volume and noise. In addition, the interaction between different design parameters is not fully considered in traditional methods, which may result in missed opportunities for overall performance improvement.
2. Hypoid Gear Optimization Design Mathematical Model
2.1 Design Variables
The design variables for hypoid gear optimization are crucial as they directly influence the performance of hypoid gear pair. As shown in Table 1, the independent parameters include the number of teeth of the pinion z1, the outer diameter of the large gear de2, the face width of the large gear b2, the offset distance E, and the spiral angle of the large gear β2. These variables are selected because they have a significant impact on the volume and noise characteristics of the hypoid gear. For example, the number of teeth affects hypoid gear ratio and the size of hypoid gear, while the offset distance influences the meshing characteristics and load distribution.
| Design Variable | Symbol |
|---|---|
| Number of teeth of pinion | Z1 |
| Outer diameter of large gear | de2 |
| Face width of large gear | b2 |
| Offset distance | E |
| Spiral angle of large gear | β2 |
2.2 Objective Functions
2.2.1 Minimizing Gear Pair Volume
The volume of the hypoid gear pair is an important consideration as it affects the material cost and the overall size of the transmission system. The objective function for minimizing the volume is formulated as follows:
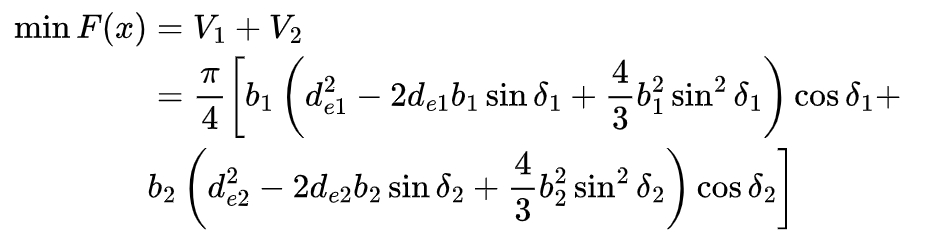
where V1 and V2 are the volumes of the pinion and the large gear, respectively, b1 and b2 are the face widths of the pinion and the large gear, de1 and de2 are the outer diameters of the pinion and the large gear, and δ1 and δ2 are the pitch cone angles of the pinion and the large gear.
2.2.2 Minimizing Noise
Noise is a critical factor in the performance of hypoid gear, especially in applications where quiet operation is required. The objective function for minimizing noise is based on the relationship between the coincidence coefficient and the noise level. When the coincidence coefficient εF approaches 2, the gear pair meshing noise is minimized. The objective function is given by:
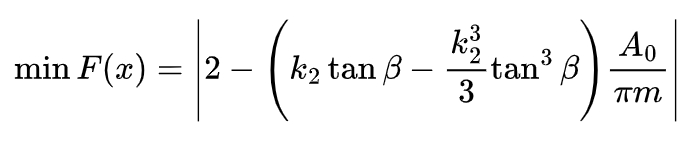
where K2 is a coefficient, is the average spiral angle of hypoid gear, A0 is the pitch cone distance, and m is the module of the large gear.
2.3 Constraint Conditions
2.3.1 Gear Tooth Number Constraints
The number of teeth of hypoid gear has a significant impact on the meshing performance and noise level. To ensure smooth transmission and reduce noise, the sum of the number of teeth of the pinion and the large gear should be within a certain range. As shown in Table 2, the constraints are set as follows:
| Constraint | Lower Limit | Upper Limit |
|---|---|---|
| Number of teeth of pinion z1 | 8 | 12 |
| Number of teeth of large gear z2 | 30 | – |
| Sum of teeth z1+z2 | 40 | 60 |
2.3.2 Offset Distance Constraints
The offset distance affects the meshing characteristics and load distribution of the hypoid gear. If the offset distance is too large, it may lead to increased tooth surface wear and potential undercutting. Therefore, the offset distance is constrained as follows:
0.1dα2 ≤ E ≤ 0.2de2
where is the reference diameter of the large gear.
2.3.3 Face Width Constraints
Increasing the face width can improve the coincidence coefficient and reduce noise, but it also increases the volume of hypoid gear pair. Therefore, the face width is constrained to balance these two factors:
4m ≤ b2 ≤ 10m
2.3.4 Spiral Angle Constraints
The spiral angle affects the meshing performance and axial force of hypoid gear. A larger spiral angle can increase the coincidence coefficient and improve the smoothness of meshing, but it also leads to increased axial force. The spiral angle is constrained as follows:
30° ≤ βm ≤ 50°
where βm is the average spiral angle.
2.3.5 Strength Constraints
To ensure the reliability and durability of the hypoid gear, strength constraints are imposed. The bending strength calculation safety factor SF should be greater than or equal to the allowable minimum safety factor SFmin, and the contact fatigue strength calculation safety factor SH should be greater than or equal to the allowable minimum safety factor SHmin.
3. Optimization Solution Based on Multi-Objective Genetic Algorithm
3.1 Multi-Objective Optimization Problem
When dealing with multiple objective functions, such as minimizing volume and noise simultaneously, the optimization problem becomes more complex. Unlike single-objective optimization, there is no single solution that can optimize all objectives simultaneously. The optimal solution is usually a set of solutions, known as the Pareto front. In the case of hypoid gear optimization, the volume and noise objectives often conflict with each other. For example, reducing the volume may lead to an increase in noise, and vice versa. Therefore, finding the best compromise between these two objectives is the key to the optimization process.
3.2 NSGA-II Algorithm
The NSGA-II (Non-dominated Sorting Genetic Algorithm II) is a powerful algorithm for solving multi-objective optimization problems. It was proposed to improve the performance of the original NSGA algorithm. The NSGA-II algorithm uses a non-dominated sorting approach to rank individuals in the population based on their fitness values for each objective. This ranking helps in identifying the Pareto front. In addition, the algorithm incorporates a crowding distance metric to maintain the diversity of the population. By favoring solutions with a larger crowding distance, the algorithm ensures that a wide range of solutions is explored, preventing premature convergence to a single solution. The selection, crossover, and mutation operators in NSGA-II are similar to those in traditional genetic algorithms, but the non-dominated sorting and crowding distance calculations make it more suitable for multi-objective optimization.
3.3 MATLAB Implementation
In this study, the MATLAB optimization function gamultiobj is used to implement the NSGA-II algorithm. The function takes the objective function, design variables, constraints, and other parameters as inputs. The initial population size, number of generations, and other algorithm parameters are set to control the optimization process. For example, the initial population size is set to 150, and the algorithm is run for 1000 generations. The Pareto front coefficient and crowding distance are adjusted to obtain the optimal solution. The gamultiobj function returns the Pareto optimal solutions and their corresponding objective function values. These solutions can then be analyzed and selected based on the specific requirements of the design.
4. Optimization Design Example
4.1 Initial Parameters
The initial parameters of the hypoid gear pair are given in Table 3. These parameters are used as the starting point for the optimization process.
| Parameter | Value |
|---|---|
| Transmission ratio i | 4.1 |
| Number of teeth of pinion zi | 10 |
| Face width of large gear b2 | 30mm |
| Offset distance E | 20mm |
| Outer diameter of large gear de2 | 200mm |
| Spiral angle of large gear βm2 | 37.14° |
4.2 Optimization Results
The optimization results obtained using the NSGA-II algorithm are presented in Table 4. The Pareto front graph shows the trade-off between the volume and noise objectives. The points on the left side of the graph represent solutions with larger volume but lower noise, while the points on the right side represent solutions with smaller volume but higher noise. After careful consideration, a solution with a coincidence coefficient difference of around 0.05 is selected as the optimized result.
| Design Method | Number of Teeth of Pinion | Outer Diameter of Large Gear (mm) | Offset Distance (mm) | Face Width of Large Gear (mm) | Spiral Angle of Large Gear (°) | Gear Pair Volume (mm^3) | Coincidence Coefficient |
|---|---|---|---|---|---|---|---|
| Traditional Design | 10 | 200.00 | 20.00 | 30.00 | 37.14 | 2.1552 | |
| Optimization Design | 10 | 196.99 | 19.72 | 26.13 | 38.51 | 1.9532 |
4.3 Comparison and Analysis
By comparing the traditional design and the optimized design, it can be seen that the optimized design achieves a significant reduction in volume. The volume of hypoid gear pair is reduced by approximately 12.7% compared to the traditional design. At the same time, the coincidence coefficient of the optimized design is closer to the ideal value for minimizing noise. This indicates that the optimization design not only reduces the size and cost of hypoid gear pair but also improves the noise performance. The selection of the optimized solution is based on a comprehensive consideration of both volume and noise objectives, providing a practical and effective design option for hypoid gear.
5. Conclusion
5.1 Optimization Effectiveness
The application of the NSGA-II algorithm in the optimization design of hypoid gear has proven to be highly effective. By minimizing the volume of hypoid gear pair and reducing noise, the overall performance of the hypoid gear has been significantly improved. The optimized design not only meets the strength and functional requirements but also achieves better performance in terms of size, weight, and noise. This is of great significance for the application of hypoid gear in various mechanical transmissions, especially in automotive differentials where compactness and quiet operation are crucial.
5.2 Design Efficiency and Cost Reduction
The use of the NSGA-II algorithm in optimization design has also improved the design efficiency. Compared to traditional trial-and-error methods, the algorithm can quickly explore a large number of design solutions and find the optimal Pareto front. This reduces the design cycle and saves time and cost. In addition, by optimizing hypoid gear parameters, the material cost can be reduced due to the smaller volume of hypoid gear pair. This makes the design more economical and competitive in the market.
5.3 Significance and Future Research Directions
The research results of this article provide a theoretical basis for the subsequent design improvement of hypoid gear. The optimization method and process can be applied to other similar gear designs, providing a reference for improving the performance of hypoid gear transmissions. Future research can focus on further exploring the influence of other factors on hypoid gear performance, such as the influence of manufacturing errors and lubrication conditions. In addition, improving the optimization algorithm to handle more complex design requirements and constraints is also an important research direction. Overall, the optimization design of hypoid gear is an area with great potential for research and application, and continuous efforts are needed to improve the performance and reliability of hypoid gear.
