There may be four kinds of motion forms in gear transmission non-linear system: periodic motion, double periodic motion, quasi-periodic motion and chaotic motion.There are excitation frequency_-rate and other frequencies in periodic and double periodic motion, and the frequency components are commonable.If the frequency is fractional times_/n of the excitation frequency, the subharmonic response will occur, and if the frequency is m_, the superharmonic response will occur, where m and N are all integers.
Superharmonic resonance exists more or less in general nonlinear systems, while subharmonic response occurs only under certain conditions.When damping exists in the system, damping only affects the amplitude of superharmonic resonance and prevents the occurrence of subharmonic resonance as long as damping is greater than a certain value.
Quasi-periodic motion, also called quasi-periodic motion and almost periodic motion, has two or more frequency components in the corresponding non-linear vibration response.Mathematically, no matter how small the positive number e is, it can always be found that the positive number L=L(e), so that at least one gamma(e) can be found in each interval of length L, which satisfies the inequality.
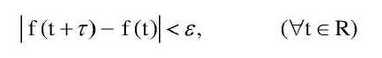
Chaos motion is a kind of seemingly random and complex irregular motion occurring in deterministic system, which is highly sensitive to initial conditions and impossible to predict for a long time.The characteristics of chaos are as follows: globally, the points of chaotic motion seem to fill a certain area, which is limited. This area is called chaotic attractor of system. The strange attractor of chaotic motion has infinite self-similar structure; locally, the two tracks whose initial conditions are close together, and the speed of final separation is exponential times, also known as the butterfly effect.
Combining the above two points, it can be seen that the attractor’s orbit needs to be folded so that the chaotic motion can achieve overall stability while overcoming the butterfly effect.
