Helix angle is an important structural parameter of helical gear, and it is also the main factor causing time-varying contact line. The existence of helix angle makes helical gear produce an axial coincidence degree. The analysis of the change law of time-varying contact line with helix angle provides a relevant basis for the subsequent study of time-varying friction and friction torque. In this paper, 10 °, 15 °, 20 °, 25 ° and 30 ° are selected in the common range of helix angle to analyze the change of the root mean square of contact line and the fluctuation rate of contact line length, and further study the characteristics of contact line.
The change rule of the root mean square of the dimensionless contact line length with different helix angles is shown in Figure 1. Within the range of 10 ° to 30 °, the root mean square of the contact line length decreases with the increase of the helix angle. This is because the helix angle becomes larger, the axial coincidence degree becomes larger, the end face coincidence degree becomes smaller, and the overall coincidence degree becomes larger. However, as a result, the width of the meshing plane becomes smaller, the pressure angle of the base circle becomes larger, and the tooth pitch of the end face becomes larger, resulting in less number and shorter length of contact lines, making the total number of contact lines on the whole smaller.

The ratio of the difference between the maximum value and the minimum value of the contact wire length to the maximum value of the contact wire length is defined as the fluctuation rate of the contact wire length:
The length fluctuation of contact lines with different helix angles is shown in Figure 2:

Figure 2 shows that the maximum fluctuation occurs when the helix angle is 15 °, and the minimum fluctuation occurs when the helix angle is 20 ° and 30 °. As shown in Figure 3, at the initial time, when the maximum values (end face pitch) of L1 and L3 are equal, and the sizes of L2 and L4 are equal, the length of the entire contact line does not change, and the helical gear runs most smoothly. This is because with the increase of L3, the length of the first contact line becomes longer, the length of the nth contact line becomes shorter, and the length change of the two contact lines is equal, which has no effect on the total length change of the whole contact line. The length of the I contact line increases, and the length of the j contact line decreases. The changes of the two lines are the same, which has no effect on the total length change of the whole contact line. As shown in the table, the dimensionless values of L1, L2, L3 and L4 of each helix angle at the initial time.
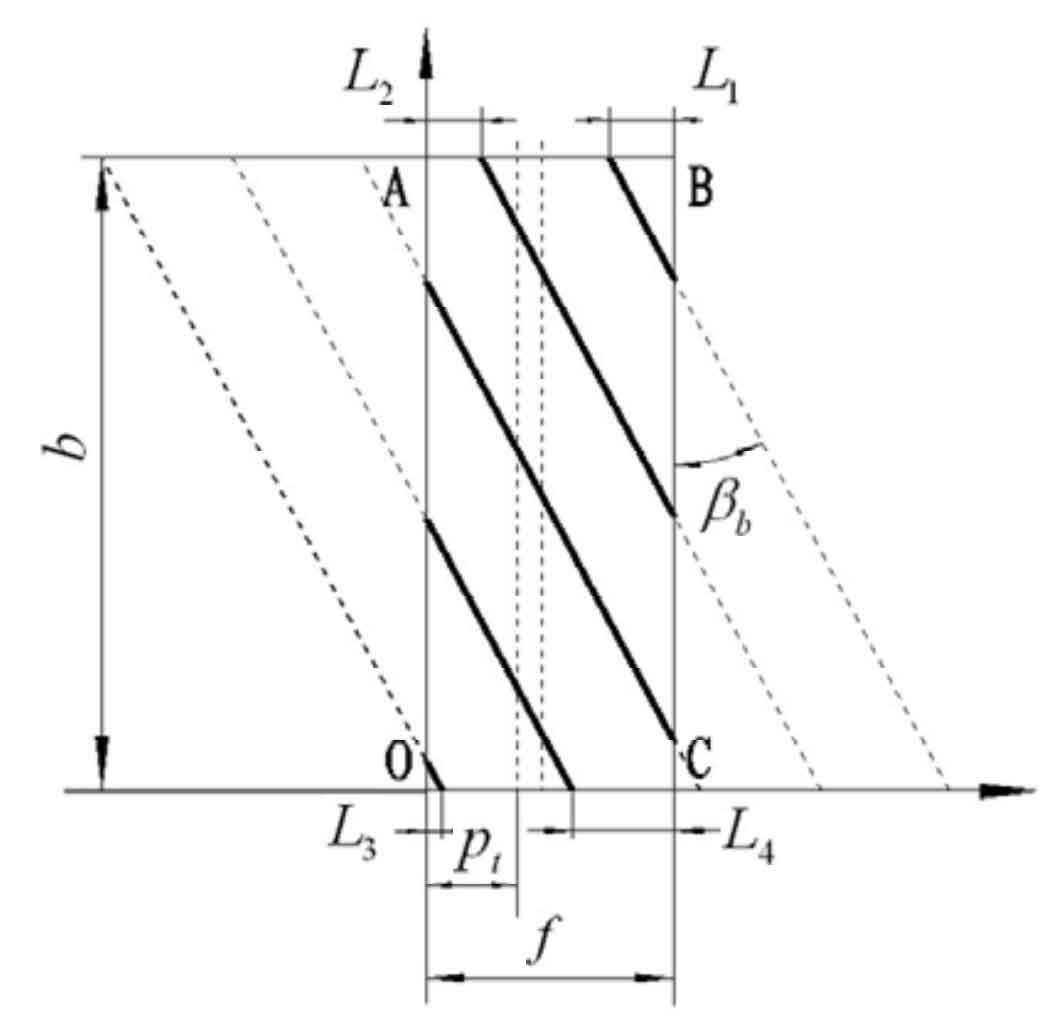
The maximum fluctuation occurs when the helix angle is 15 °, because L3 is much larger than L1, and the length of L2 and L4 is the same, which makes the first contact line increase all the time. The two factors make the total contact line length sharply larger, which makes the fluctuation value larger. The small fluctuation of 20 ° and 30 ° is because the length of L1 is similar to that of L4. When the nth contact line moves out of the meshing area, the length of the ith contact line passing through point C will not change for a period of time. The length of the j contact line decreases, and the length of the 1 contact line increases. The increase and decrease are equal, so that the change of the whole contact line length is small, and its fluctuation is small.
| β (°) | L1 | L2 | L3 | L4 |
| 10 | 0.102 | 0.006 | 0.160 | 0.970 |
| 15 | 0.019 | 0.089 | 0.162 | 0.092 |
| 20 | 0.089 | 0.006 | 0.167 | 0.083 |
| 25 | 0.157 | 0.086 | 0.173 | 0.071 |
| 30 | 0.052 | 0.005 | 0.181 | 0.057 |
From the end face, the meshing state of the helical gear is exactly the same as that of the spur gear. Therefore, the end face coincidence can be calculated by using the end face meshing angle, end face pressure angle and the number of teeth of the driving and driven gears εα , The end face coincidence degree of helical gear is also between 1 and 2. Because the tooth width of the helical gear is B, when a pair of gears are meshed at the front end face, the different sections of the tooth width are still meshing, that is, the axial coincidence degree of the helical gear is formed εβ 。 Due to tooth width B and helix angle β There is no limit, so the coincidence degree of helical gears can reach a large value, which is also an important reason for the smooth transmission of helical gears.
