The tooth trend of the involute helical gear is the helix angle, and the normal tooth profile is in the vertical direction of the involute helical gear, which is different from the involute tooth profile of the end face. Therefore, there are two different tooth profiles in two directions, which need to be represented by two groups of parameters, namely, the end face parameters and the normal face parameters. The plane perpendicular to the gear axis is often called the end face, and the involute tooth shape is the origin of its name. The main tooth profile parameters of the end face in the theoretical design.
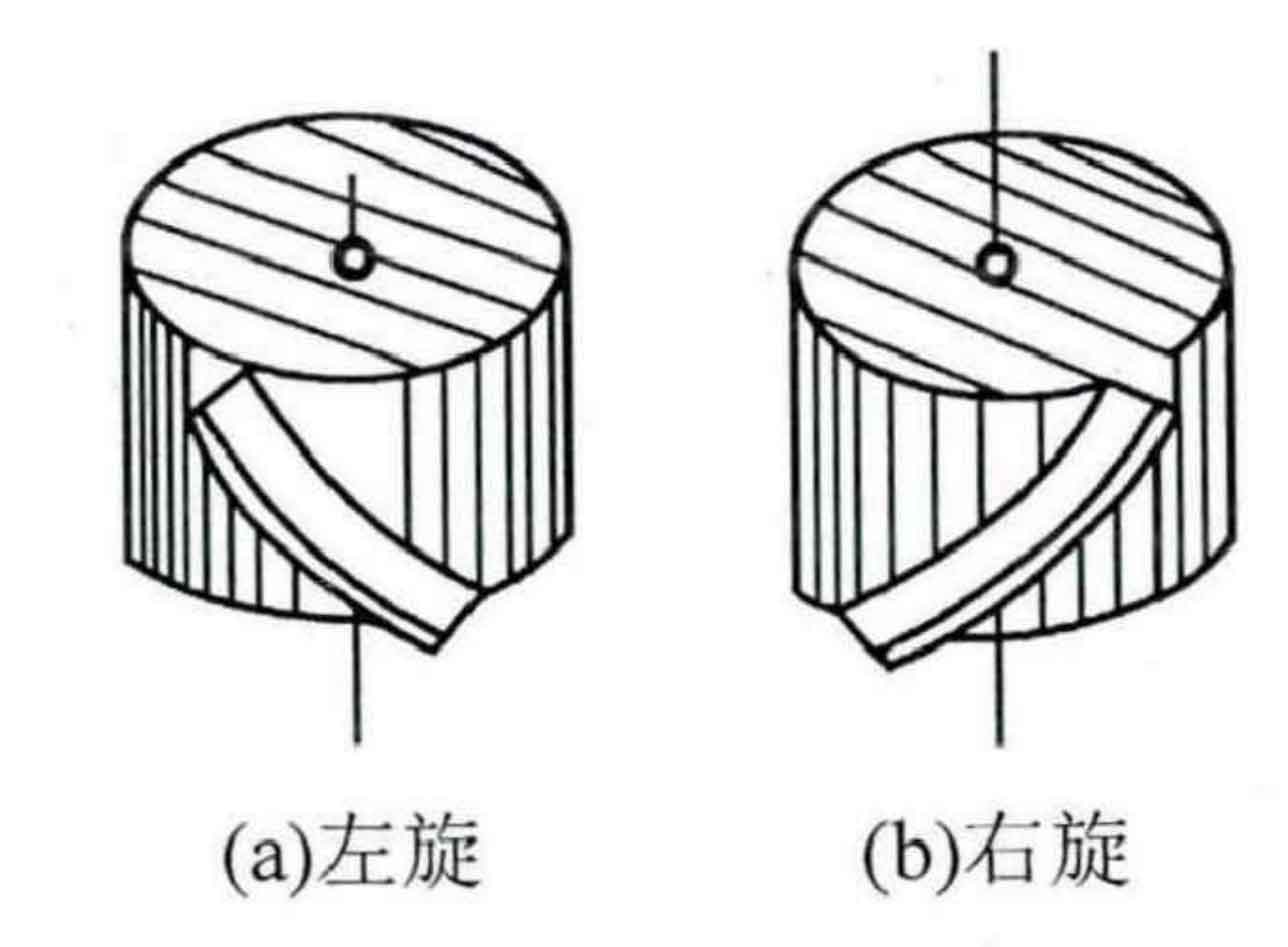
The plane perpendicular to the spiral is often called the normal plane. Main tooth profile parameters of normal surface in theoretical design. Helix angle: as shown in Figure 1, the included angle between the tangent of the helix and the axis of the helical gear is the helix angle, as shown in Figure 1.
(1) Relationship between normal modulus and end modulus
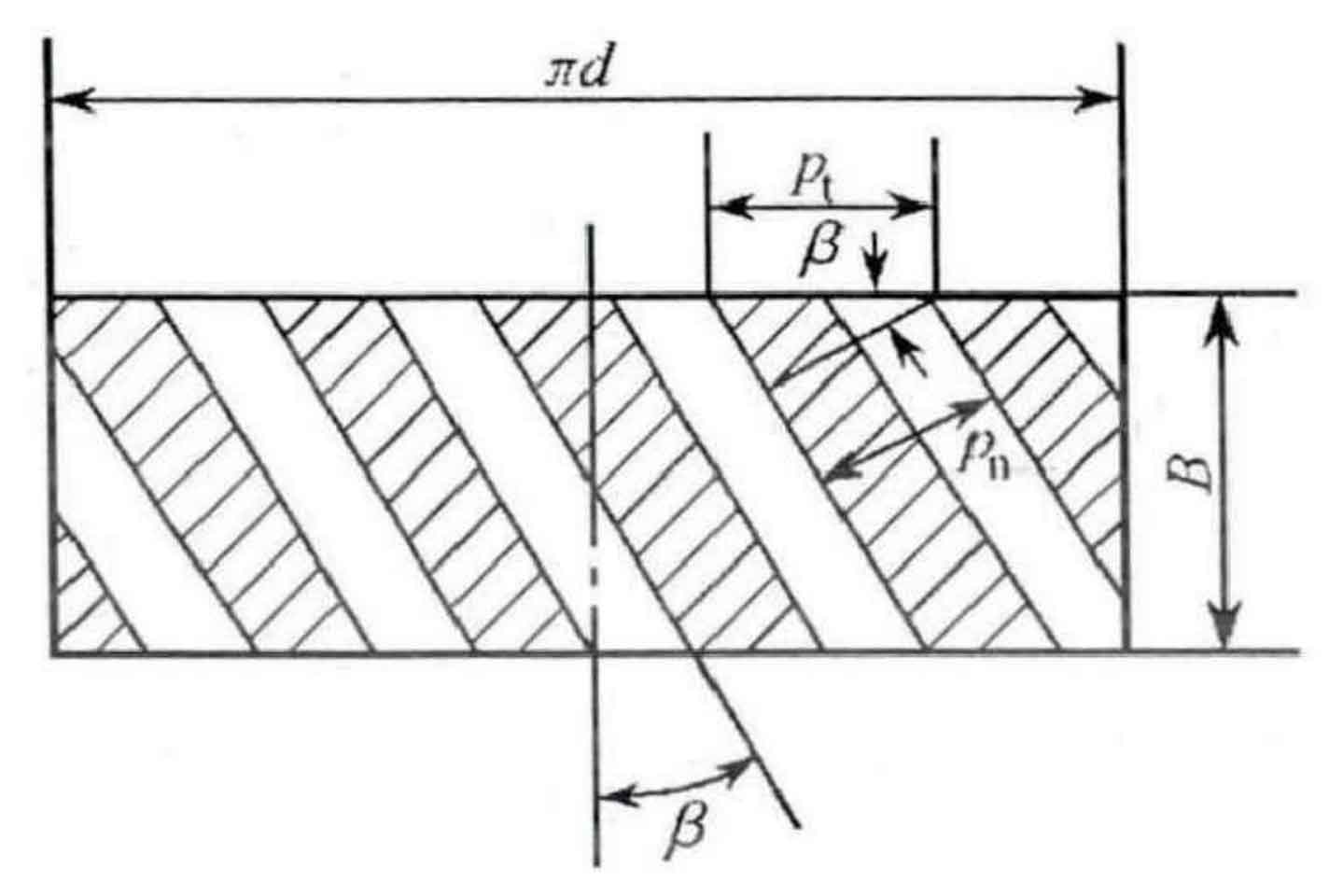
As shown in the relationship between normal surface modulus and end surface modulus in Figure 2, Pt is the end surface pitch, and PN is the normal surface pitch.
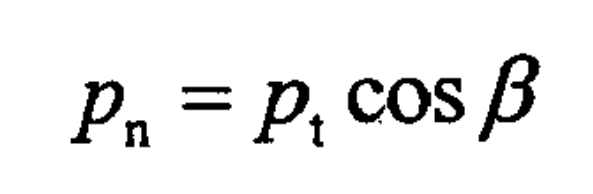
Therefore, the relationship between the face module and the end module of the helical gear method can be obtained as follows:
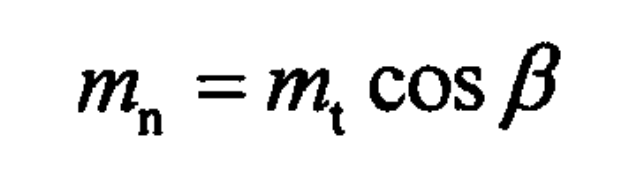
(2) Backlash coefficient and addendum height coefficient
These two coefficients are important parameters. From the angle of normal direction or end face, it can be found that the addendum height and backlash are the same, as follows:
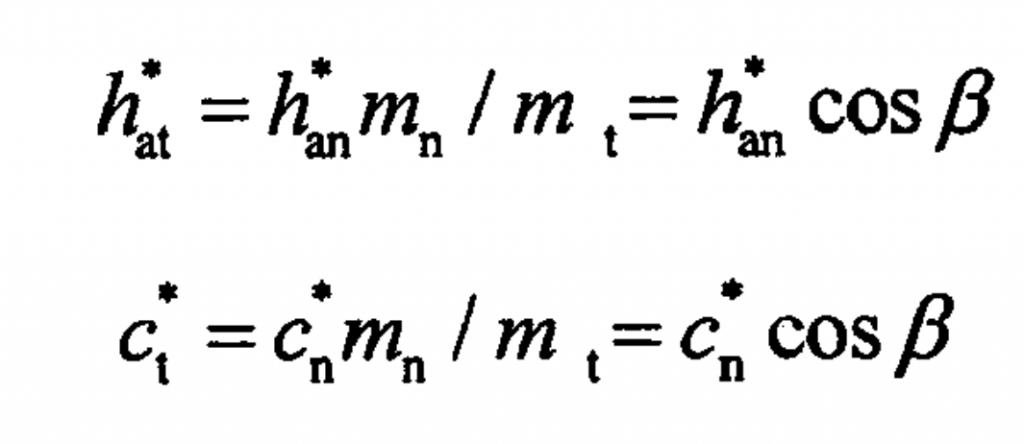
(3) Normal face and end face pressure angle
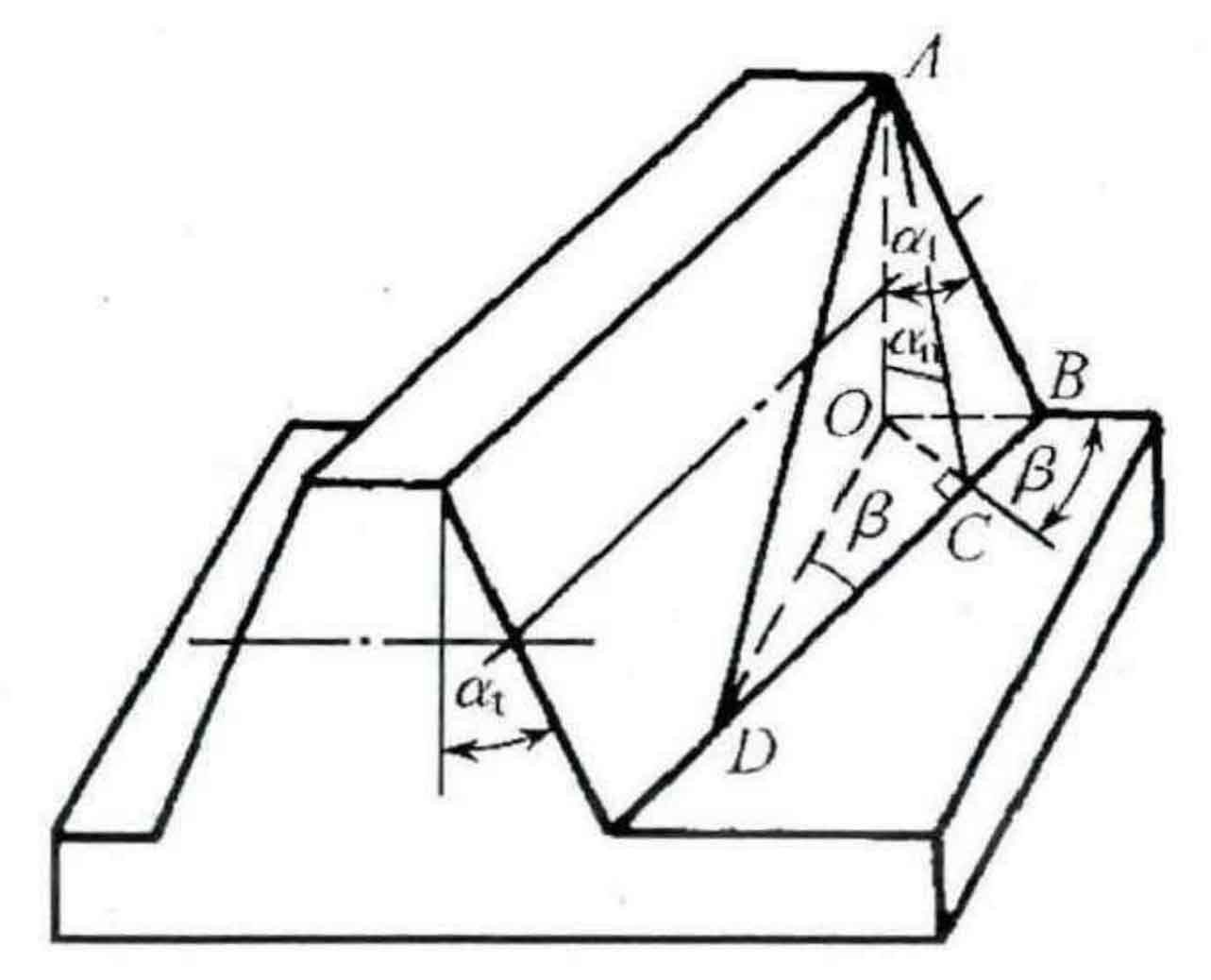
The normal pressure angle of cylindrical gear can be obtained by helical gear α N and face pressure angle α T.
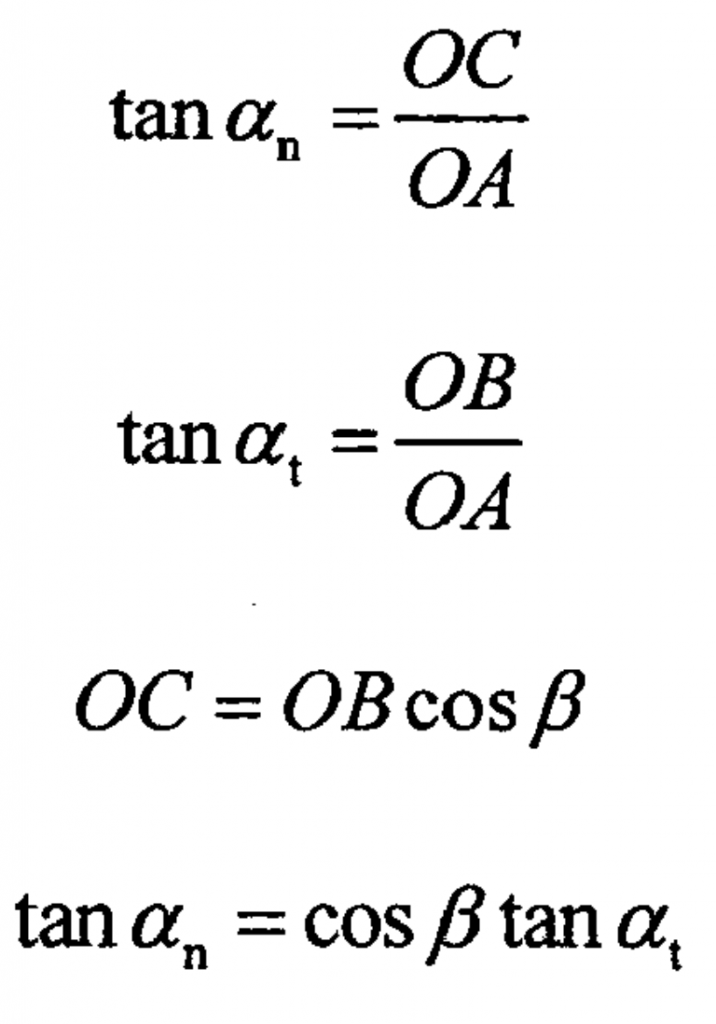
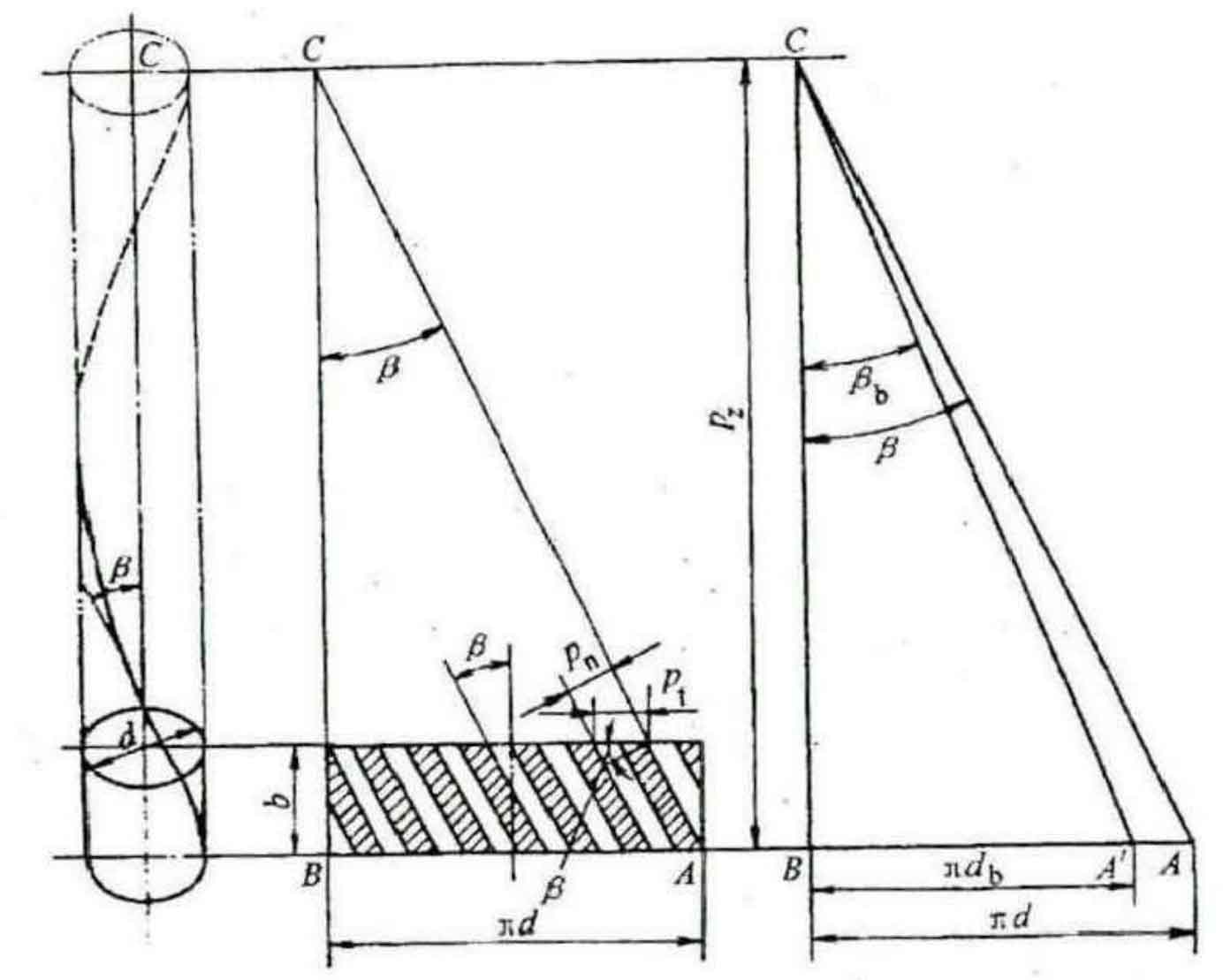
(4) Figure 4 Schematic diagram of cylindrical helix angle, helical gear indexing cylindrical helix angle β Helix angle with base cylinder β B relationship:
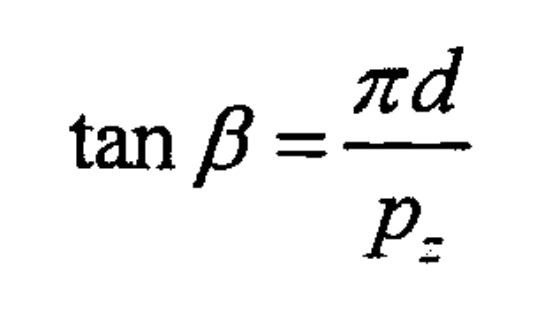
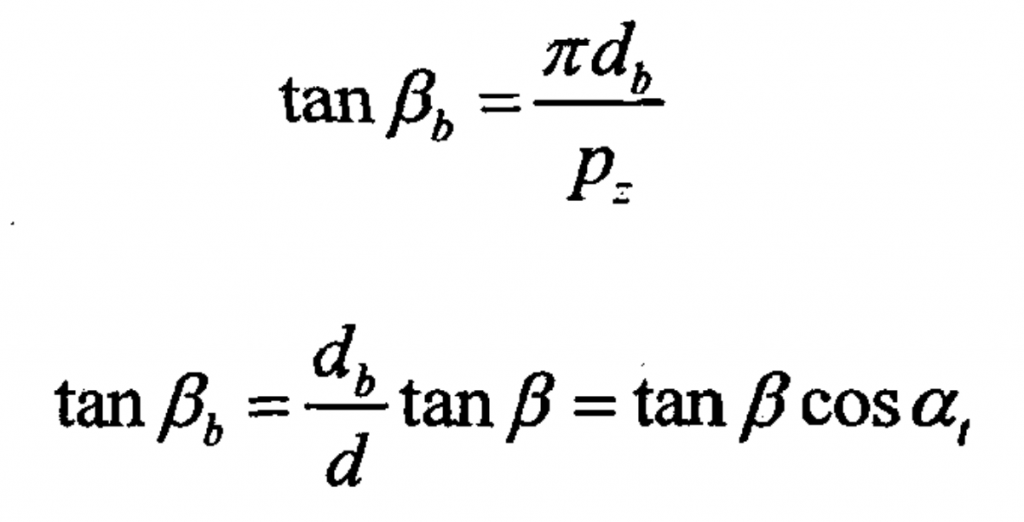
(5) The relationship between the end face displacement coefficient and the normal face displacement coefficient is as follows
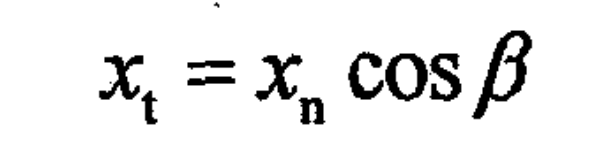
It can be seen that the center distance parameter and helix angle of helical gear transmission β With strong correlation. When the module and tooth number of helical gear are determined, change the helix angle β The size of can be matched with the center distance.
