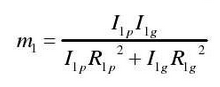Taking a high-speed helical gear transmission of an electric vehicle as the research object, the structure diagram is shown in Figure 1. The power of the motor is directly input into the reducer, and then transmitted to the vehicle half shaft after two-stage helical gear deceleration. In order to study the vibration characteristics of single-stage high-speed helical gear transmission, a 6-DOF bending torsion shaft dynamic model of input stage teeth pair in the figure is established, as shown in Fig. 2.
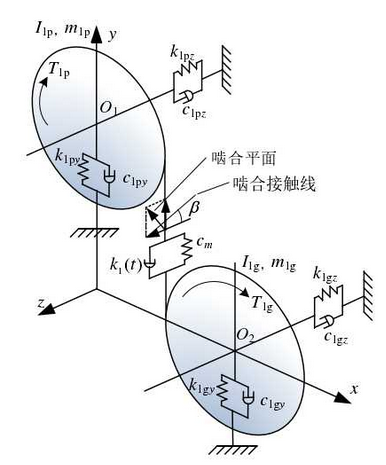
The differential equations of dynamic model in Fig. 2 are listed as follows:
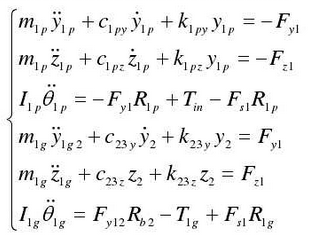
Among them, M1P and m1g are the mass of the input gear pair; R1p and r1g are the base circle radius of the input gear pair; tin is the system input torque; T1G is the input gear torque; y1p and z1p are the vibration displacement of the input stage pinion in the Y and Z directions; y1g and z1g are the vibration displacement of the input stage gear in the Y and Z directions; and θ 1p and θ 1g are the vibration displacement of the input stage gear in the Y and Z directions Is the torsional displacement of the input end teeth to the two gears; K1y and k1z are the equivalent support stiffness in Y and Z directions of the input stage pinion; k23y and k23z are the equivalent support stiffness in Y and Z directions of the intermediate shaft; c1y and c1z are the equivalent support damping in Y and Z directions of the intermediate shaft; c23y and c23z are the Y and Z direction of the intermediate shaft respectively FS1 is the meshing impact force of the input tooth pair.
Based on the force and displacement decomposition, the tangential and axial dynamic meshing forces of the input end pairs are expressed in the form of parameters, as shown in the formula
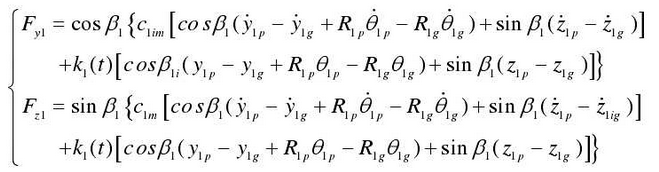
Where K1 (T) is the time-varying meshing stiffness of the input tooth pair; β 1 is the helical angle of the input end tooth pair; α is the pressure angle; and CM1 is the meshing damping of the input end tooth pair.
The calculation of meshing damping is shown in the formula
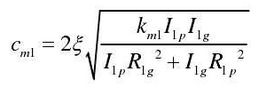
Where: ζ is the damping ratio, which is taken as 0.1 in this paper.
In order to eliminate the influence of gear rigid body angular displacement on the follow-up analysis, the relative angular displacement q is introduced and the angular displacement is transformed into linear displacement
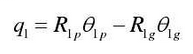
The torsional vibration equation can be simplified as follows
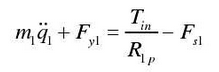
Where M1 is the equivalent torsional mass of the input end tooth pair, and its expression is shown in the formula