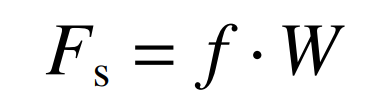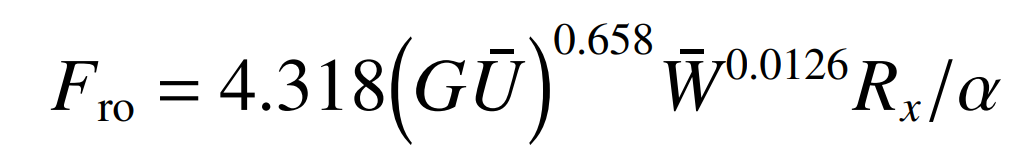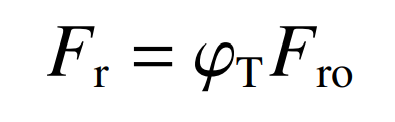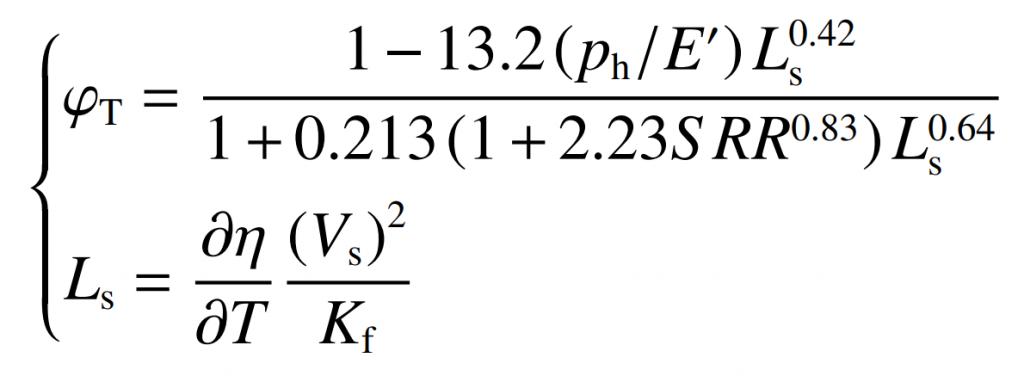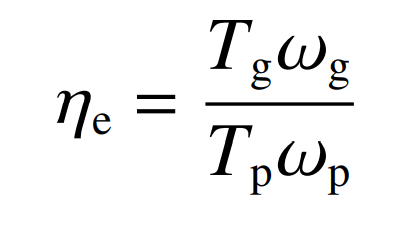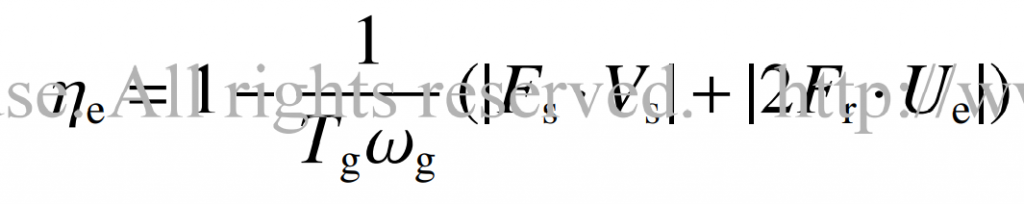After the sliding friction coefficient at the instantaneous meshing position of spiral bevel gear is solved by the formula, the sliding friction is calculated by the following formula:
The friction between spiral bevel gear tooth surfaces includes rolling friction and sliding friction. Due to the particularity of spiral bevel gear tooth surface contact, it is difficult to solve the rolling friction considering the influence of velocity vector and entrainment angle The rolling friction in spiral bevel gears is usually simulated by the line contact lubrication model. The rolling friction is studied by this method. The isothermal rolling friction is:
Where: α Is the viscosity pressure coefficient, dimensionless material parameter G= α E ‘, dimensionless coiling speed u, dimensionless load parameter W. different from spur gear, the relative sliding speed between the tooth surfaces of spiral bevel gear is relatively large. In order to consider the influence of friction heat on rolling friction coefficient, the heat influence factor is introduced φ t. Then the rolling friction is expressed as:
Where φ T is defined as:
In the above formula, KF is the thermal conductivity of lubricating oil.
The instantaneous transmission efficiency of spiral bevel gear is defined as:
Where: TG and TP are the torque of large wheel and small wheel, ω G and ω P is the speed of the big wheel and the small wheel If only friction loss is considered, the sum of instantaneous transmission efficiency is expressed as: