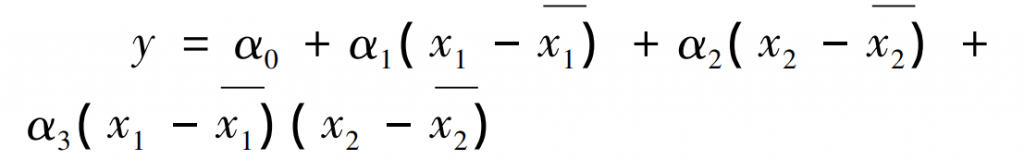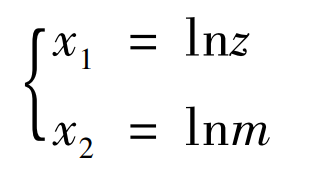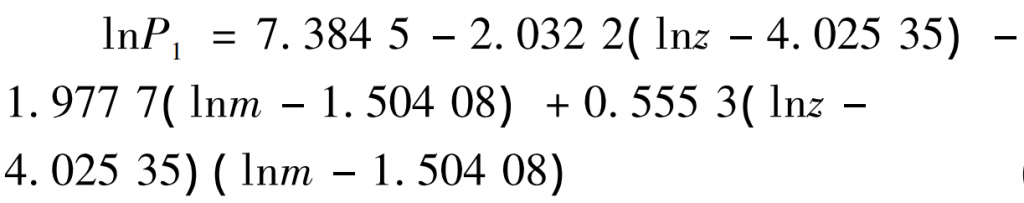The relationship between dependent variables and regression analysis is a kind of modeling technology. The experiment involves four independent variables, and the units of independent variables are different, which brings some difficulties to the structural analysis of regression equation. For multiple linear regression, the data should be centralized first to eliminate the influence of different dimensions and orders of magnitude. When selecting the regression model, in addition to considering the interaction between two independent variables, it may also need to consider the interaction between three or four independent variables. However, a large number of practices show that high-order interactions often do not exist or are small and can be ignored. Therefore, the following principles are adopted: ensure the main effect of each variable and estimate the interaction between two independent variables as much as possible. Since it is impossible to give the structure of interaction between independent variables directly, the centralized one-time nonlinear regression model is adopted. The model is:
Where: X1 and X2 are the mean values of independent variables X1 and X2 respectively.
In view of the research results in this paper, the geometric constraint of the tooth width and the natural tooth angle have no significant influence on the natural frequency of the double tooth. In order to obtain a more concise regression equation of natural frequency, the regression equation with the number of teeth Z and modulus m of double circular arc gear as independent variables is established.
| Source of variation | Sum of squares | Freedom | Mean square | F | Significance probability p |
| Number of teeth | 15 902 290. 49 | 3 | 5 300 763. 50 | 14. 032 | 0. 029 |
| Modulus | 22 809 386. 35 | 3 | 7 603 128. 78 | 20. 127 | 0. 017 |
| Helix angle | 3 317 203. 84 | 3 | 1 105 734. 61 | 2. 927 | 0. 201 |
| Tooth width | 1 185 038. 64 | 3 | 395 012. 88 | 1. 046 | 0. 486 |
| Error | 1 133 264. 03 | 3 | 377 754. 68 | / | / |
| Total | 44 347 183. 35 | 15 | / | / | / |
By analyzing the values of dependent variables and independent variables in Table 1, it can be seen that there is a large difference between the values of dependent variables and independent variables. If the regression analysis is carried out directly, the regression coefficient and standard error will be large and the fitting degree will be poor. The determination coefficients corresponding to the original value, second power, third power, square root, reciprocal and natural logarithm of the first-order natural frequency and the number of teeth are calculated respectively. The results are shown in Table 2.
| P1 | P 2 1 | P3 1 | ■P1 | 1 /P1 | lnP1 | |
| z | 0. 97 | 0. 918 | 0. 866 | 0. 988 | 0. 875 | 0. 996 |
| z2 | 0. 954 | 0. 896 | 0. 861 | 0. 977 | 0. 986 | 0. 993 |
| z3 | 0. 944 | 0. 886 | 0. 823 | 0. 969 | 0. 984 | 0. 986 |
| ■z | 0. 965 | 0. 922 | 0. 871 | 0. 977 | 0. 938 | 0. 976 |
| 1 / z | 0. 971 | 0. 919 | 0. 865 | 0. 990 | 0. 974 | 0. 997 |
| lnz | 0. 967 | 0. 913 | 0. 858 | 0. 988 | 0. 980 | 0. 998 |
The determination coefficient is used to determine the fitting degree of the regression line, that is, the fitting degree between the predicted value generated by the least square regression method and the actual observation data. The larger the determination coefficient is, the better the fitting degree is. In Table 2, the maximum coefficient of determination is 0 998 is fitted by the natural logarithm lnz of the number of teeth of double circular arc gear and the natural logarithm lnp1 of natural frequency, f = 674 495, the corresponding significance test probability p is 0 000, less than 0 001, it can be seen that the natural logarithm of the number of teeth has a significant impact on the natural logarithm of the natural frequency. That is, the form of the dependent variable of the final regression equation (the first-order natural frequency of the constrained mode) is lnp1.
Similarly, the parameters of all independent variables that determine the maximum value of the coefficient are as follows:
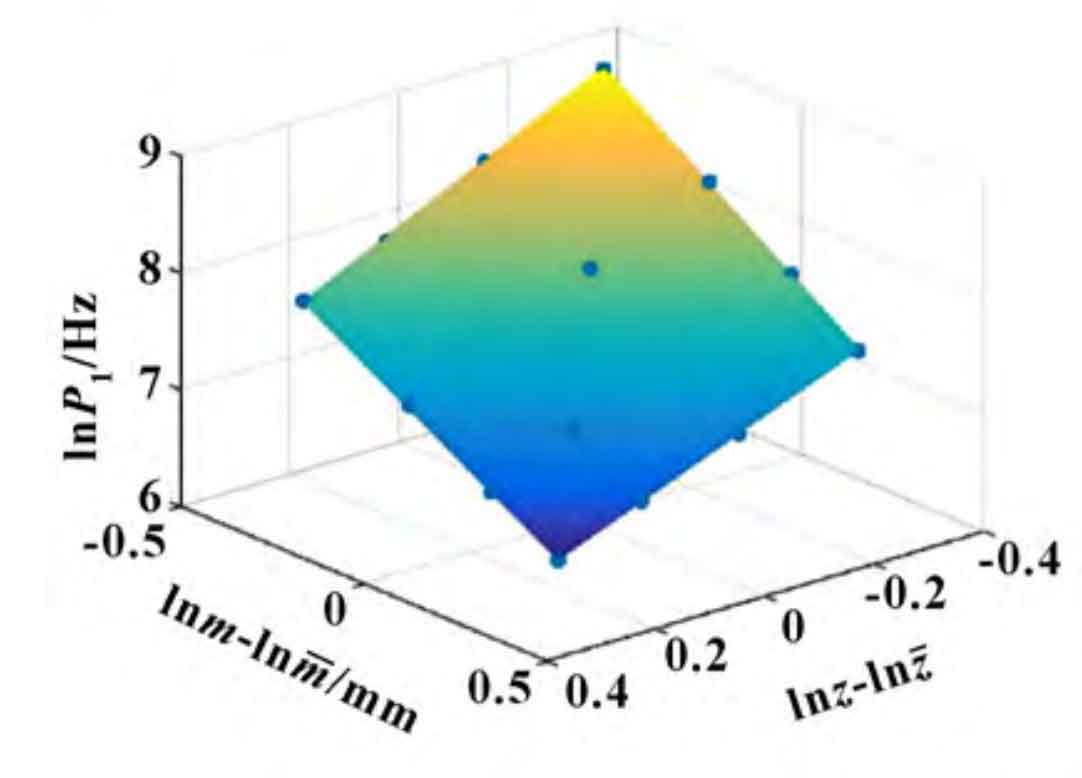
The data about the number of teeth Z, modulus m and frequency P1 in Table 1 are substituted into the formula and regression equation model formula respectively. The regression command in MATLAB software is used to calculate the data-centered multiple nonlinear regression, and the determination coefficient r = 0 998 9 、F =3 511. 5、P = 0. 000, draw the response surface, as shown in Figure 1, and determine the final regression equation as:
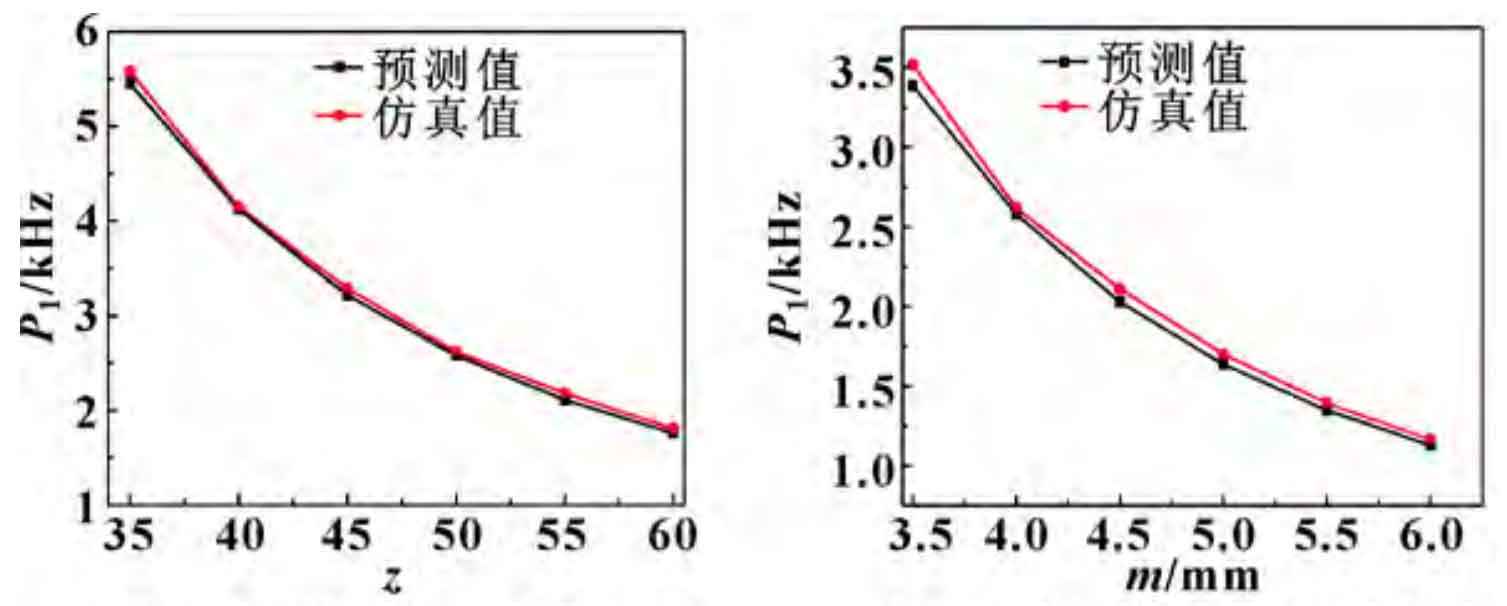
In addition, take the number of teeth z = [35, 60], modulus M = [3 5, 6] mm, helix angle β = 20 °, tooth width b = 45 mm, double circular arc gear model is established according to the above parameters. Using the numerical modal method, the first-order frequency under the constrained mode is solved, and the predicted value of the regression equation is compared. The results are shown in Figure 2. It can be seen that the error between the solved value and the predicted value is small. Combined with the regression equation and response surface, the regression surface fitting is good.