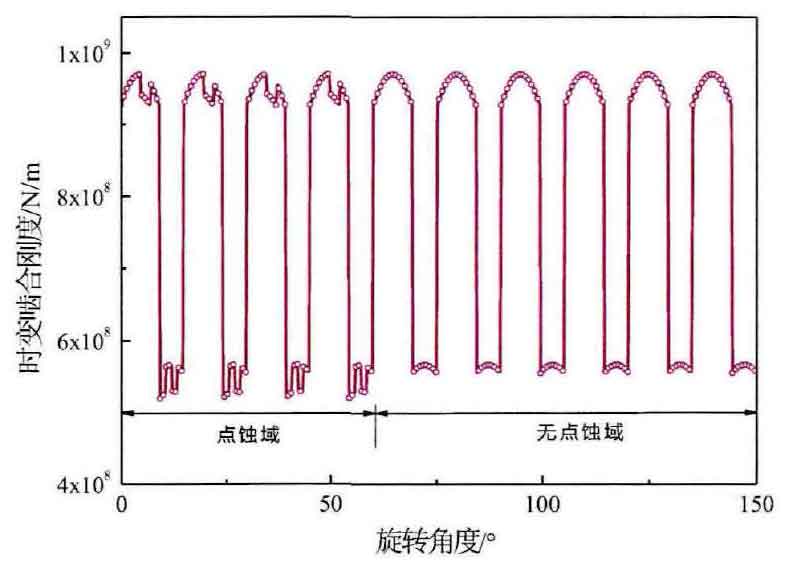
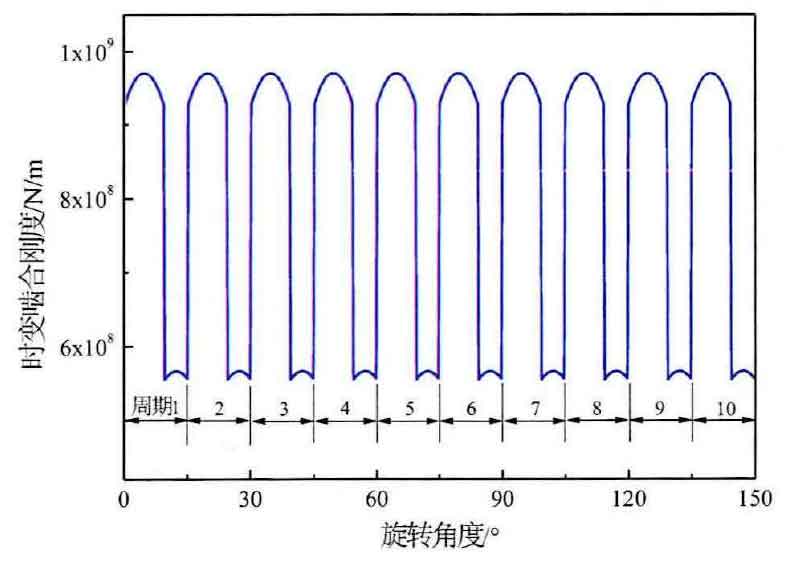
According to the above research on the time-varying meshing stiffness of gears with pitting features, the periodic stiffness curve with pitting features in Figure 1 is drawn. As shown in the figure, the meshing stiffness of the first four teeth is set with pitting features, and the meshing stiffness of the last six teeth is without pitting features. One gear meshing period in Fig. 2 and Fig. 1 is selected to analyze the stiffness reduction effect of the pitting feature, and the average stiffness method is used to select the double meshing area and the single meshing area for stiffness comparison. The comparison results of the average stiffness of the double meshing zone and the single meshing zone with and without pitting show that the stiffness reduction percentage is 0.82% in the double meshing zone and 3.1% in the single meshing zone.
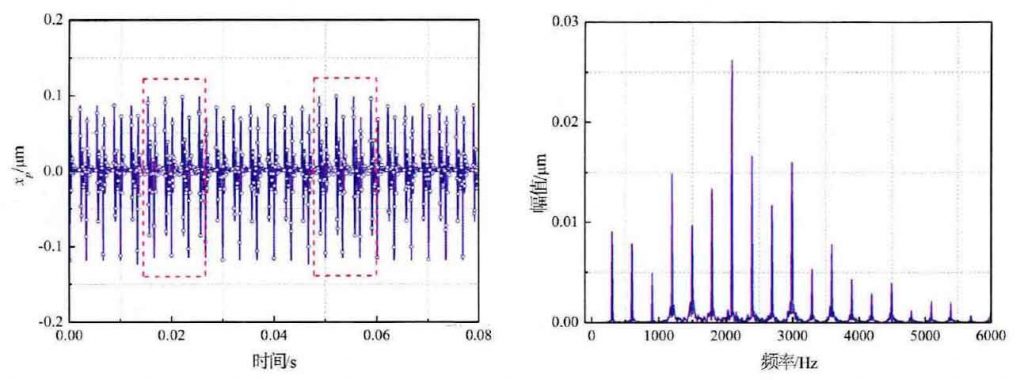
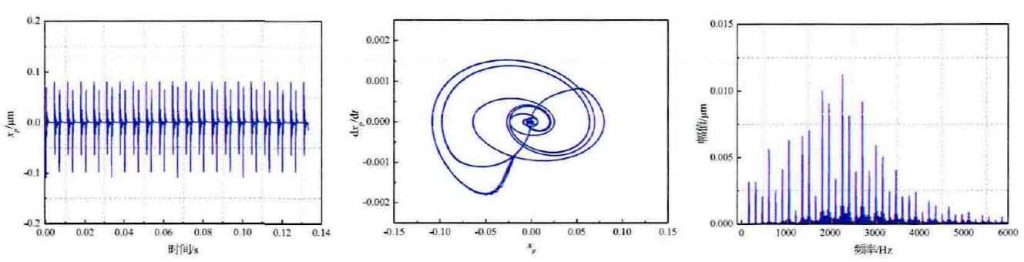
According to the effect of time-varying meshing stiffness of gear pair under pitting characteristics shown in Fig. 1, the Runge Kutta (ode45) numerical algorithm is still used to simulate the vibration differential equation of the formula. The time domain diagram and frequency domain diagram of xp under the action of pitting characteristics are drawn in Fig. 2. The displacement response of driving gear in Fig. 3 (a) can be roughly seen that the displacement response amplitude increases in the pitting area, as shown in the rectangular box marked area in the figure. Compared with the statistical index G1, the displacement amplitude of the marked area is 0.1 μ m, and the displacement amplitude of the unmarked area is 0.085 μ m, and the increase percentage of the amplitude is 17.6%. The statistical index of displacement amplitude shows that the amplitude of displacement response of driving gear increases due to the effect of tooth surface pitting, which leads to the unbalanced response of the system. At the same time, due to the periodic effect of gear rotation, its displacement response also presents periodic vibration effect. In the same way, the displacement spectrum response Figure 4 (c) without pitting characteristics and the spectrum response Figure 3 (b) with pitting characteristics are compared. The results show that the displacement response amplitude under the same frequency also increases significantly.
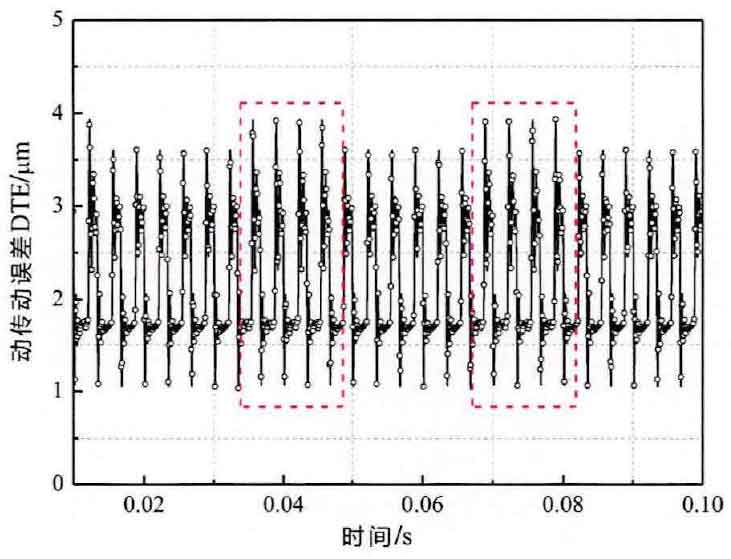
The time-domain curve of DTE response under pitting characteristics is plotted in Fig. 5. It can be roughly seen that the amplitude of marked area of rectangular box in the figure is significantly increased compared with that of unmarked area, and it shows periodic change, which is similar to the effect of amplitude change in Fig. 3 (a). The G statistic index of rectangle marked area is 3.92 μ m, while the 仏 statistic index of non marked area is 3.60 μ m, and the amplitude increase percentage is 8.9%. The numerical results show that pitting causes the unstable response of DTE between gear pairs, and the unstable response also changes periodically due to the rotation periodicity of gears.
To sum up, when the pitting occurs on the tooth surface, the system will produce local unbalanced dynamic response characteristics, such as the increase of response amplitude, the decrease of meshing stiffness and so on. The performance of these unbalanced response characteristics paves the way for the research of gearbox fault diagnosis and monitoring in the later stage. In engineering application, the vibration output response signal of the system should be monitored in real time, and the dynamic response of the gear system should be monitored comprehensively. In case of abnormal characteristics, the shutdown detection and maintenance should be carried out in time, so as to realize the rapid fault diagnosis and detection of the gear box, and reduce the probability of accident occurrence and abnormal profit loss as much as possible.