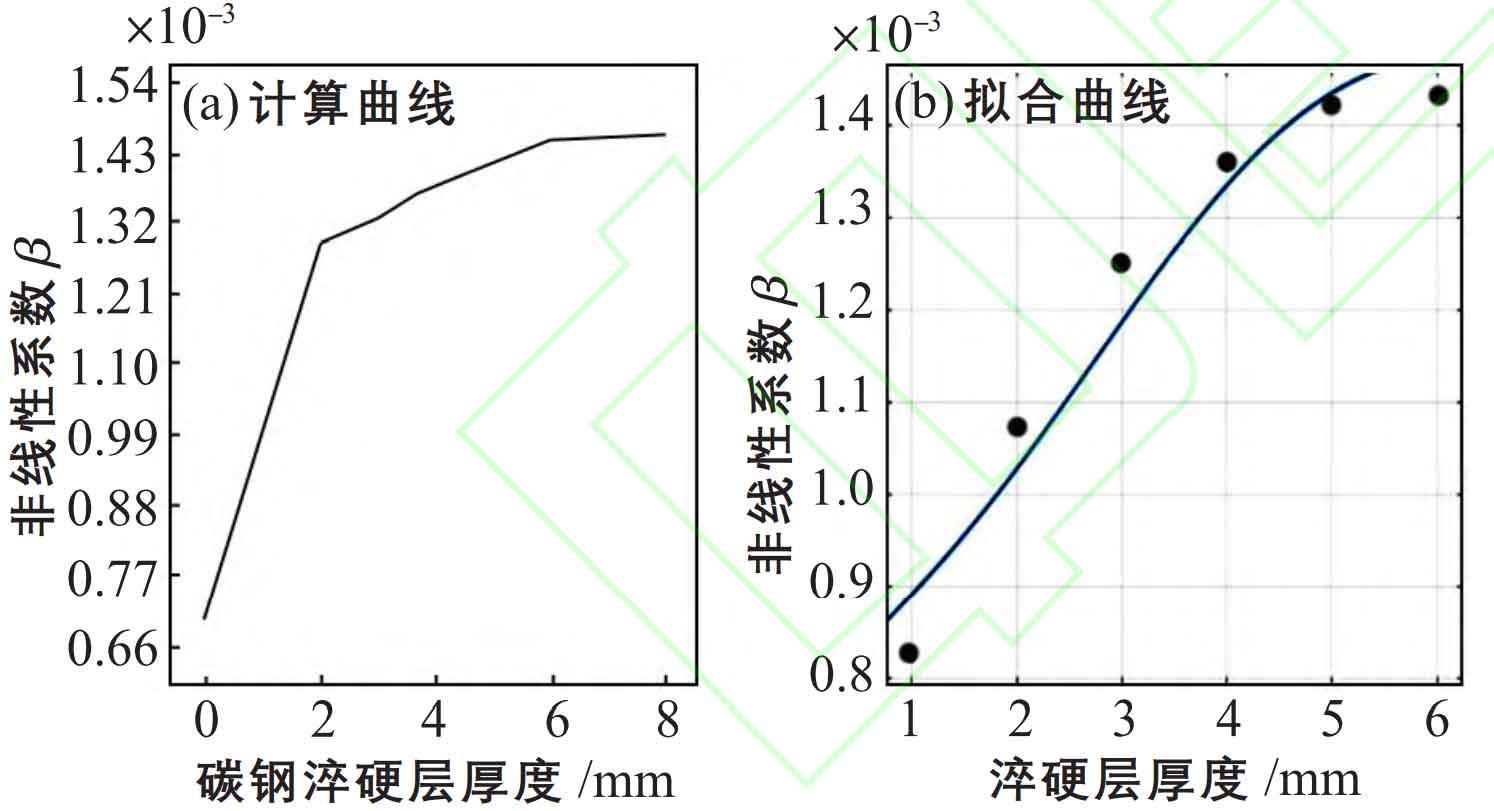
According to the formula, the nonlinear ultrasonic coefficients of different samples are calculated according to the amplitude of the fundamental wave and the second harmonic wave. The amplitude of fundamental wave and second harmonic of carbon steel gears with different hardened layer thicknesses are shown in the table. It can be seen from the observation table that, with the continuous increase of the hardened layer thickness of carbon steel gears, the basic wave amplitude value presents a growing trend, and the corresponding second harmonic of the sample also gradually increases. The ultrasonic amplitude attenuation degree is accompanied by the increase of the hardened layer thickness, which indicates that the amplitude of the ultrasonic signal has a good resolution to the hardened layer thickness, and the relationship between the nonlinear ultrasonic coefficient and the hardened layer thickness is established, as shown in the figure.
| Sample No | Hardened layer thickness/mm | Fundamental wave amplitude/V | Second harmonic amplitude/V | Nonlinear coefficient |
| 1# | 0 | 47.81 | 1.76 | 0.00070 |
| 2# | 2 | 60.00 | 4.65 | 0.00129 |
| 3# | 3 | 86.79 | 10.05 | 0.00133 |
| 4# | 4 | 93.67 | 12.08 | 0.00138 |
| 5# | 6 | 98.87 | 13.90 | 0.00145 |
| 6# | 8 | 143.70 | 29.56 | 0.00146 |
The ultrasonic nonlinear coefficient shows a growing trend with the increase of the hardened layer thickness of carbon steel gears. The metallographic analysis of corresponding samples shows that the microstructure of carbon steel gears after quenching is more dense, the crystal structure density of materials is larger, and they are more sensitive to the transmission of ultrasonic signals. The samples without quenching treatment have smaller crystal density, larger crystals, and larger gaps between crystals, which is not conducive to the transmission of ultrasonic signals. The ultrasonic nonlinear coefficient of carbon steel gears increases rapidly when the thickness of hardened layer is 0~2 mm; When the thickness of hardened layer is 2~4 mm, the growth rate of ultrasonic nonlinear coefficient of carbon steel gear is smaller than that when the thickness of hardened layer is 0~2 mm; When the thickness of hardened layer is 4~6 mm, the growth rate of nonlinear coefficient continues to decrease gradually; When the thickness of the hardened layer is 6~8mm, the nonlinear ultrasonic coefficient still shows a decreasing trend. By extracting the growth rate of the relationship between the ultrasonic nonlinear coefficient and the hardening layer thickness, the effect of predicting the hardening layer thickness of the sample can be achieved, and the characterization of the ultrasonic nonlinear coefficient on the material hardening layer thickness can be realized. Linear regression operation has the characteristics of accuracy, stability and strong filtering, and is widely used in the synthesis of data formulas. In order to accurately characterize the relationship between the ultrasonic nonlinear coefficient and the hardening layer thickness of the sample, the linear regression calculation model is used to fit the relationship between the hardening layer thickness of carbon steel gears and the ultrasonic nonlinear coefficient (Figure (b)). The fitted formula is:

In the formula, the value range of a is [-0.0001826, 0.0002749], the average value of the range is selected, and the value of a is 0.00005986; The value range of b is [-0.00001562, -0.000000843], and the interval average value is selected. The value of b is -0.00000823; The value range of c is [0.001,248, 0.001,944]. Select the average value of the interval, and the value of c is 0.001,596. The fitting formula can be used to characterize the hardened layer thickness of carbon steel.
