Fatigue strength constraint
The nutation bevel gear adopts the basic tooth profile of GB / T 12759-1991 double circular arc cylindrical gear, and the calculation formula of bending fatigue strength of tooth root is as follows

Where T1 is the transmission torque of the gear; Ka is the service factor; kV is the dynamic load coefficient; K1 is the load distribution coefficient between the contact traces; KF2 is the load distribution coefficient in the contact trace; μ ε is the integral part of the coincidence degree; K Δ ε is the contact trace coefficient; ye, Yu, y β, YF, yend are the material elastic coefficient, tooth number ratio coefficient, spiral angle coefficient, tooth shape coefficient and tooth end coefficient of bending strength. The integral part of coincidence degree μ ε can be expressed as follows:
The contact fatigue strength of the tooth surface is as follows:
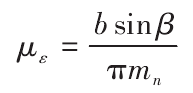
Where KH2 is the load distribution coefficient in the contact trace; Ze, Zu, Z β and Z α are the material elastic coefficient, tooth number ratio coefficient, helix angle coefficient and contact arc length coefficient of contact strength respectively.

The constraint functions of tooth root bending and tooth surface contact fatigue strength are as follows:

Tooth number constraint
There is no undercutting phenomenon in the double circular arc spiral bevel gear, and there is no limit on the number of teeth. However, if the number of teeth is too small, it will cause low coincidence degree and unstable transmission. Therefore, the number of teeth Z1 > 5 is generally required. At the same time, in order to reduce the swing excitation force of nutation drive, the tooth difference of meshing gear is less than 4, and the number of teeth of nutation outer bevel gear is less than that of inner bevel gear. The constraint function of tooth number is as follows:

Radial dimensional constraints
According to the requirement that the radial dimension of the reducer should not exceed 108 mm, and considering the influence of factors such as the thickness of reducer box, the diameter of indexing circle at the big end of internal bevel gear is Dei ≤ 90 mm

Tooth width factor constraint
If the tooth width factor φ D needs to satisfy 15 ≤ φ d = BD1 ≤ 13, then the constraint function of tooth width coefficient is as follows:

Helical angle constraint
Considering the stability of the transmission, if the helix angle is 20 ° < β < 40 °, the constraint function of the spiral angle is as follows:

Coincidence degree constraint
The integral part of coincidence degree μ ε = 1 ~ 6, and the constraint function is as follows:

