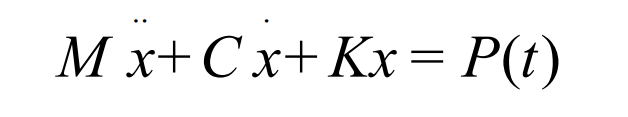The finite element static analysis method can be used to analyze the load contact of spiral bevel gear in detail, but this method does not consider the influence of dynamic factors on the meshing characteristics of spiral bevel gear. The periodic change of meshing teeth will not only lead to the change of meshing stiffness, but also affect the friction between meshing tooth surfaces. The tooth surface contact characteristics at different positions calculated through multiple static contact analysis can not fully reflect the dynamic meshing characteristics in the process of spiral bevel gear transmission. The dynamic contact analysis of spiral bevel gear considers the impact effect and other factors in the meshing process, and the simulated meshing transmission process is closer to the reality.
Compared with static contact analysis and dynamic contact analysis, their common point is that they should meet both normal and tangential contact conditions on the meshing tooth surface. The difference between them is that the process of dynamic contact analysis depends on time, is also affected by geometric nonlinear conditions, and the kinematic and dynamic states on the contact surface are unknown. At the same time, the inertia force term and damping force term are added to the finite element equation of dynamic analysis. The structural dynamic behavior of nonlinear dynamics mainly depends on the nonlinear behavior of the structure itself and the applied load conditions. Therefore, in order to accurately simulate the actual working conditions and obtain the dynamic meshing characteristics of spiral bevel gears at different meshing positions, it is necessary to conduct dynamic loading contact analysis on spiral bevel gears after completing the static loading contact analysis.
Acceleration plays an important role in dynamic problems. The load and response of the structure change with time. Because the structure consumes energy in motion, the damping factor needs to be considered when dealing with dynamic problems. At present, the understanding of damping mechanism at home and abroad is not very clear, and it is difficult to accurately simulate damping. In application, the damping matrix of the structure is sometimes regarded as Rayleigh damping formed by linear combination of mass matrix and stiffness matrix.
The meshing force and response of dynamic meshing of spiral bevel gears change with time. The dynamic equation is:
Where m is the mass matrix, x, X and x represent the node displacement, velocity and acceleration in turn, C represents the damping matrix, K represents the stiffness matrix, and P (T) represents the load vector.