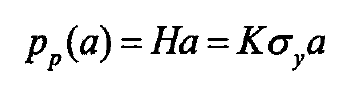According to the two-dimensional contour curve (formula) of rough surface expressed by W-M function, the morphology characteristics of rough surface are approximately simulated and characterized by fractal parameters D, G and γ, and the contour curve of micro geometry of rough surface is transformed from physical characteristics to mathematical model.
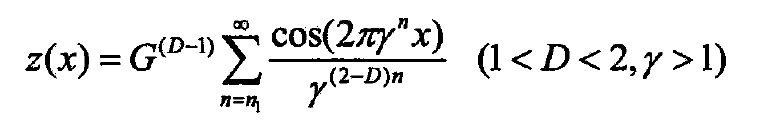
Where:
Z (x) – 2-D contour curve value of rough surface, m;
D-fractal dimension;
G-height parameter of rough surface (roughness amplitude for short);
The characteristic parameter of γ – fractal is generally taken as γ = 1.5.
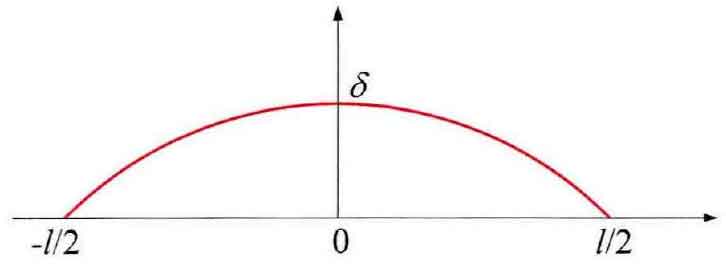
Based on the W-M fractal function and the scale independence of fractal parameters, the elastic-plastic fractal contact M-B model of rough surface is established, and the contact equivalent is simplified as the contact between rough surface and rigid ideal surface, as shown in Figure 1. It can be clearly seen in the figure that the deformation of rough surface under load is δ = z-d. At the same time, the distribution of cosine variation before deformation of asperity with rough surface derived from W-M function is shown in Fig. 2.
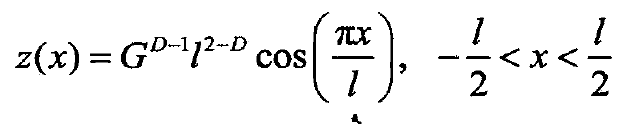
According to the cosine distribution function and graphic display of the micro convex body related to the length I, combined with the calculation method of the curvature radius of any point, and the approximate relationship between the contact area a and the contact length I, the curvature radius r can be expressed as:
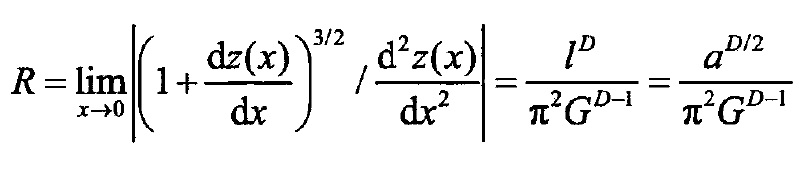
The correlation formula of the maximum deformation δ max at the top is as follows:
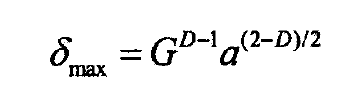
By substituting the formula of curvature radius and contact area into the formula of critical deformation δ C of elastic-plastic transformation and the relationship between curvature radius and contact area, it can be concluded that the critical deformation δ C of elastic-plastic transformation and the relationship between curvature radius and contact area are as follows:
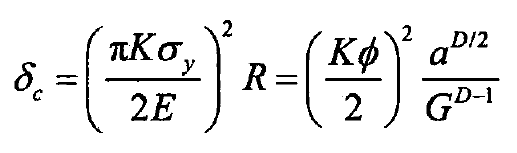
Where:
δ C is the critical deformation of elastic-plastic transformation;
σ y is the yield strength of softer materials;
E-comprehensive elastic modulus;
K is the correlation coefficient between surface hardness and yield strength, k = H / σ y;
H – surface hardness;
φ – material characteristic parameter, φ = σ Y / E.
By comparing the formulas, the critical contact area AC of elastic-plastic transformation can be deduced as follows
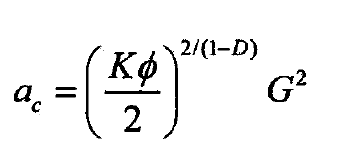
According to the contact deformation diagram of micro convex body, as shown in Fig. 3, the relationship between elastic deformation and top curvature radius can be obtained from geometric mathematical relationship
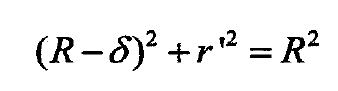
If we assume that the elastic deformation is very small, there is δ 2-0, and combine with the formula 2A = a ‘, we can further simplify the relationship between the real contact area of the micro convex body and the curvature radius of the top and the elastic deformation
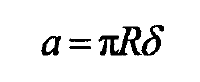
At the same time, the normal elastic load of a single asperity can be expressed as:
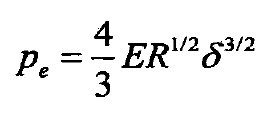
The function relation between elastic load and contact area can be obtained by substituting the related parameter relation into the formula
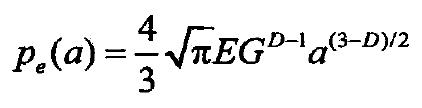
Similarly, if plastic deformation occurs, the function of plastic load with respect to contact area is as follows: