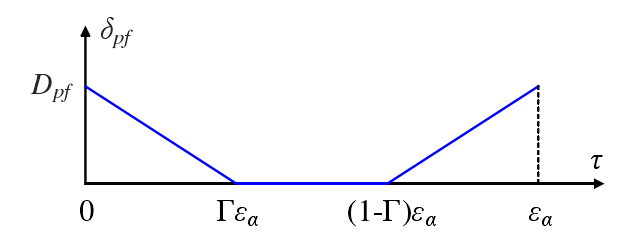
In this study, symmetrical straight line modification is used in the direction of tooth profile, and the modification curve is shown in Figure 1. The modification curve can be expressed by two parameters: DPF and dimensionless modification range. The corresponding curve equation is shown in the formula.
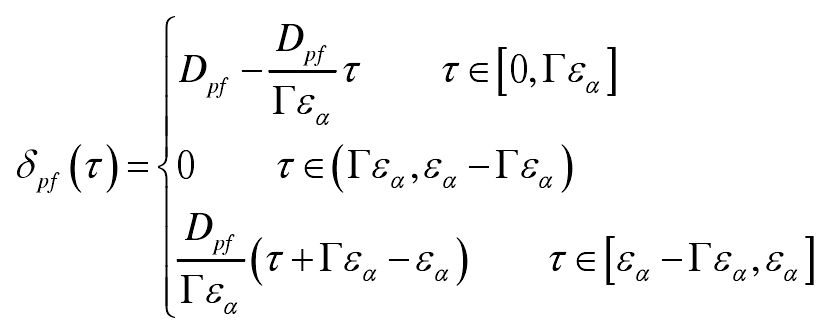
Reducing the fluctuation of static transmission error is a recognized criterion for tooth profile modification, so the calculation of static transmission error of gear pair is the key to tooth profile modification. Firstly, combined with the formula, the total load acting on the meshing pair at any meshing position is obtained
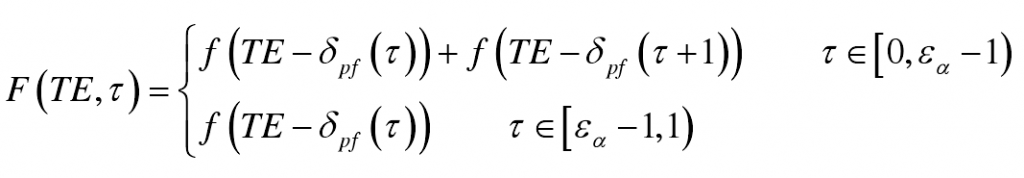
In the formula, Te is the transmission error; f (U) is the formula of single tooth meshing force, which is given by the formula; δ PF is the modification of tooth profile at any meshing position in a meshing cycle, which is given by the formula; because proper tooth profile modification can avoid the influence of external meshing of tooth line, in order to simplify the calculation, the influence of support system and large deformation of tooth on the coincidence degree ε A is not considered in the formula. Then, for the nominal meshing force ft, the static transfer error curve in one meshing period is the solution of the following problem
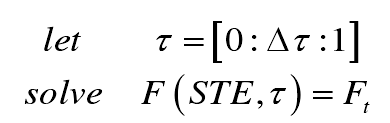
Figure 2 is the static transfer error curve of cutting gear pair 2 calculated by the above method. Fig. 2 (a) shows the static transfer error curve under different tooth direction modification amount without tooth profile modification. With the increase of tooth direction modification amount, the tooth stiffness gradually decreases and the static transfer error gradually increases. Fig. 2 (b) shows the static transmission error curve under different tooth profile modification without tooth profile modification. With the increase of tooth profile modification, the fluctuation of static transmission error first decreases and then increases. Because the profile modification does not enter the single tooth meshing zone, the static transmission error in this zone remains unchanged.
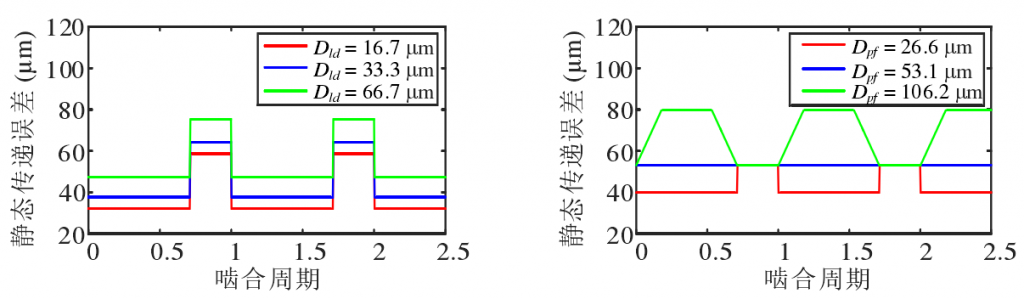
(b) Different tooth profile modification amount without tooth profile modification
Reducing the fluctuation of static transmission error is a widely accepted criterion for tooth profile modification. In practice, it is necessary to compare the fluctuation degree of different static transmission error curves. Therefore, the first thing to solve is to establish the index to quantify the fluctuation degree. According to Houser’s suggestion, the sum of the amplitude of each harmonic component in the static transfer error curve is taken as the index of its fluctuation degree. Since the higher the frequency, the smaller the amplitude of the harmonic component is, the sum of the amplitudes of the first 100 harmonic components is defined as the variable CHTE for the convenience of calculation
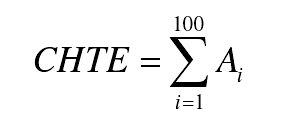
Where AI is the amplitude of the i-th harmonic component of the static transfer error curve.
Therefore, the problem of tooth profile modification becomes the following optimization problem:
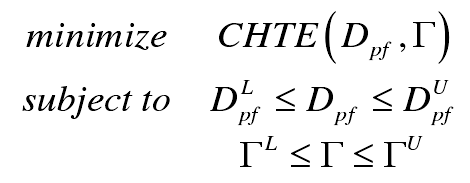
Where the superscripts L and u denote the upper and lower bounds of the variable, respectively.