In modern agricultural machinery, transmissions play a critical role in ensuring efficient power delivery under varying load conditions. Traditional tractor transmissions often rely on fixed-axis gear systems, which, while simple and cost-effective, suffer from limitations such as large physical size, limited gear ratios, and high operator fatigue due to complex shifting mechanisms. To address these challenges, I propose a novel transmission design that incorporates a face planetary gear train, enabling a compact, lightweight, and multi-speed configuration suitable for heavy-duty applications like tractors. This design leverages the unique advantages of planetary gears, including high torque density and smooth power transmission, to achieve up to 24 theoretical gear ratios through a combination of main and auxiliary transmissions. By integrating face gears with planetary arrangements, this system minimizes space requirements while enhancing performance, making it ideal for evolving agricultural needs where versatility and efficiency are paramount.
The core of this innovation lies in the use of face gears, which are typically employed in intersecting or non-intersecting shaft transmissions at 90-degree angles. Face gears offer superior performance due to their high contact ratio, leading to smoother power flow, reduced vibration, and lower noise levels compared to conventional cylindrical gears. In this transmission, face gears are combined with planet gears to form a compound planetary system that allows multiple speed ratios without changing gear engagement states. This eliminates gear shock during shifting, reduces component wear, and simplifies the overall structure. The transmission comprises a main gearbox with eight operating conditions and an auxiliary planetary gear set providing two forward and one reverse gear, resulting in a total of 24 possible gear combinations. Key components include multi-plate clutches, band brakes, and one-way clutches, which selectively engage elements to alter torque paths and achieve desired ratios.
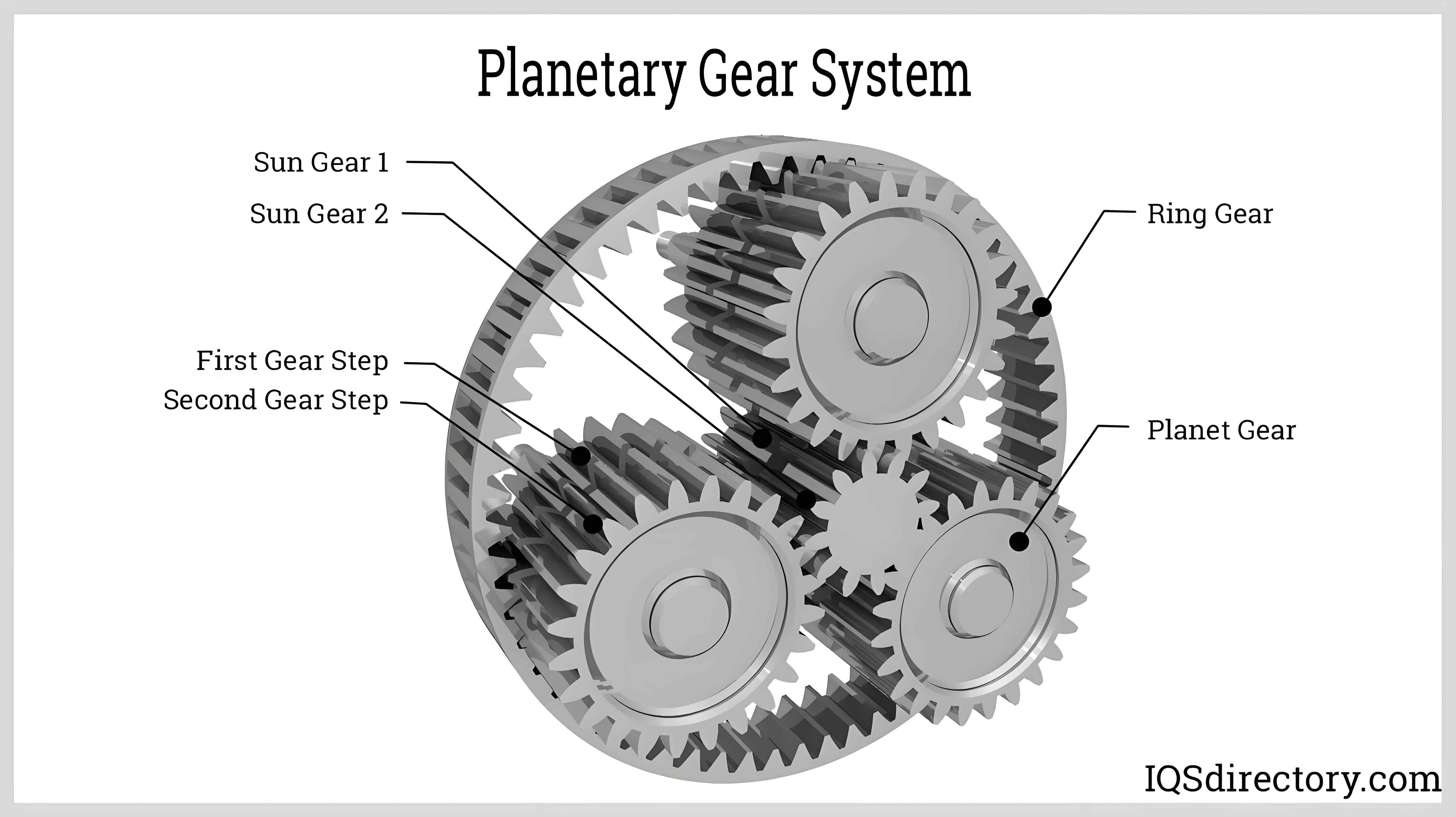
The main transmission features a cylindrical-face gear planetary system with four face gears of varying diameters and a common planetary carrier. This arrangement enables eight distinct speed ratios by controlling the engagement of clutches and brakes. For instance, when specific clutches are activated, the planetary carrier or certain face gears are fixed, altering the kinematic relationships among the planet gears. The auxiliary transmission, a single planetary gear set, further modifies these ratios to provide additional forward and reverse options. This hierarchical design ensures that the transmission can handle a wide range of operational scenarios, from low-speed high-torque tasks to high-speed transport, without compromising on compactness or reliability.
To understand the kinematic behavior, I derive the speed relationships using the fundamental equation for planetary gear systems. For a single planetary gear set, the relationship among the sun gear, ring gear, and carrier speeds is given by:
$$ n_1 + \alpha n_2 – (1 + \alpha) n_3 = 0 $$
where \( n_1 \) is the sun gear speed, \( n_2 \) is the ring gear speed, \( n_3 \) is the carrier speed, and \( \alpha \) is the characteristic parameter defined as the ratio of ring gear teeth to sun gear teeth (\( \alpha = Z_2 / Z_1 \)). This equation forms the basis for analyzing the compound system involving face gears and planet gears. In the proposed transmission, the face gear assembly can be transformed into an equivalent planetary system, allowing the application of this equation to compute speed ratios for different engagement modes.
The eight speed ratios of the main transmission are derived based on the teeth numbers of the four face gears, denoted as \( Z_4 \), \( Z_5 \), \( Z_6 \), and \( Z_7 \). The formulas for these ratios are summarized in the table below, which illustrates how selective braking and clutching operations yield distinct output speeds relative to the input.
| Operating Condition | Speed Ratio Formula |
|---|---|
| 1 | $$ \frac{Z_6}{Z_5} $$ |
| 2 | $$ \frac{Z_7}{Z_5} $$ |
| 3 | $$ \frac{Z_6}{Z_4} $$ |
| 4 | $$ \frac{Z_7}{Z_4} $$ |
| 5 | $$ \frac{Z_7}{Z_4} \times \frac{Z_4 + Z_6}{Z_6 – Z_7} $$ |
| 6 | $$ \frac{Z_7}{Z_5} \times \frac{Z_5 + Z_6}{Z_6 – Z_7} $$ |
| 7 | $$ \frac{Z_7}{Z_5} \times \frac{Z_4 – Z_5}{Z_4 + Z_7} $$ |
| 8 | $$ \frac{Z_6}{Z_5} \times \frac{Z_4 – Z_5}{Z_4 + Z_7} $$ |
These ratios are achieved by fixing different components of the planet gears system, such as the planetary carrier or specific face gears, through brakes and clutches. For example, in conditions 1–4, the planetary carrier is fixed, resulting in planet gears rotating as fixed axes, which enhances transmission efficiency. In conditions 5–6, one face gear is fixed, causing the planet gears to orbit, providing significant speed reduction and torque multiplication. Conditions 7–8 involve fixing another face gear, optimizing for high-speed output with minimal torque. The auxiliary transmission then scales these ratios further, using a single planetary set to produce additional forward and reverse gears, thereby expanding the operational range.
In designing the transmission parameters, I establish constraints to ensure structural integrity and performance. The gear teeth numbers must satisfy spatial and ratio requirements: specifically, \( Z_7 < Z_5 < Z_4 < Z_6 \) to maintain proper gear alignment and avoid interference. Additionally, the overall speed ratio range is set between 0.2 and 7.47, based on typical tractor specifications such as engine speed, wheel radius, and minimum stable velocity. Using MATLAB programming, I optimize the teeth numbers to meet these constraints, resulting in \( Z_4 = 54 \), \( Z_5 = 30 \), \( Z_6 = 74 \), and \( Z_7 = 27 \). With these values, the main transmission yields speed ratios of approximately 0.27, 0.50, 0.73, 0.90, 1.36, 1.37, 1.99, and 2.47. When combined with the auxiliary transmission, these ratios expand to 16 forward and 8 reverse gears, covering a broad spectrum of operational needs.
The selection of gear parameters, such as pressure angle and module, is crucial for durability and efficiency. I adopt a standard pressure angle of 20 degrees, which balances bending strength and contact stress resistance. The module \( m \), which determines gear size, is chosen from standardized values to ensure compatibility and reduce manufacturing costs. The relationship is defined as:
$$ m = \frac{d}{z} = \frac{p}{\pi} $$
where \( d \) is the pitch diameter, \( z \) is the number of teeth, and \( p \) is the circular pitch. Based on common standards, modules like 2, 2.5, or 3 mm are selected depending on the load requirements, ensuring that the planet gears can handle high torque without failure. The table below summarizes standard module values for reference, aiding in the selection process for similar designs.
| First Series | Second Series | First Series | Second Series |
|---|---|---|---|
| 1.00 | 1.125 | 3 | 3.5 |
| 1.25 | 1.375 | 4 | 4.5 |
| 1.50 | 1.750 | 5 | 5.5 |
| 2.00 | 2.250 | 6 | 6.5 |
| 2.50 | 2.750 | 8 | – |
Torque distribution in the planetary system is governed by the equilibrium equation:
$$ T_1 : T_2 : T_3 = \frac{-1}{\alpha + 1} : \frac{-\alpha}{\alpha + 1} : 1 $$
where \( T_1 \), \( T_2 \), and \( T_3 \) represent the torques on the sun gear, ring gear, and carrier, respectively. This relationship ensures that the planet gears efficiently distribute loads, minimizing stress concentrations and enhancing longevity. In this transmission, the use of multi-plate clutches and one-way clutches allows seamless torque transitions, reducing power loss and improving responsiveness. The one-way clutches, in particular, automate engagement and disengagement during shifts, eliminating the need for external control and preventing power cycling issues.
In conclusion, the face planetary gear train-based transmission offers a transformative solution for agricultural machinery, addressing key limitations of conventional designs. By integrating planet gears with face gears, this system achieves a high number of speed ratios in a compact footprint, reducing weight and cost while improving reliability. The kinematic analysis and parameter optimization demonstrate that the design meets practical requirements for torque and speed variation. Future work could focus on prototyping and testing to validate performance under real-world conditions, but this theoretical framework provides a solid foundation for advancing transmission technology in heavy-duty vehicles. The repeated emphasis on planet gears throughout this discussion underscores their pivotal role in enabling efficient and versatile power transmission systems.
