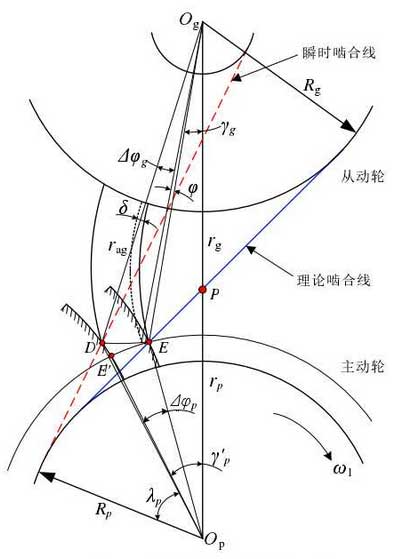
In the figure, OP is the center of the driving wheel, og is the center of the driven wheel, P is the node, D is the starting point of out of line engagement, e is the starting point of normal meshing, e ‘is the reverse point of E, and δ is the comprehensive deformation of tooth pair (obtained based on LTCA method).
In Δ opdog and Δ pdog, according to the geometric relationship, we can get the following results:

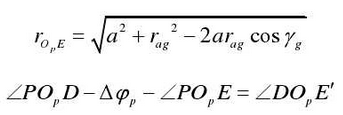
According to the simultaneous formula:
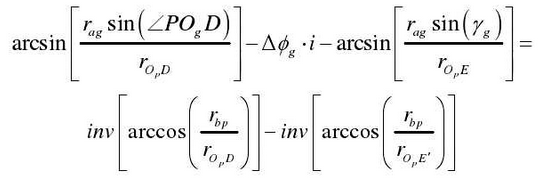
The involute equation is as follows:
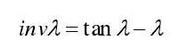
According to the simultaneous formula, the exact starting position of the out of line engagement impact can be obtained. The radius of the driven gear is the radius of the main gear, and the radius of the driven gear is the radius of the driven gear.
After the simultaneous formula is solved, the angle Δ ψ 1 of the driving wheel from the engagement point to the normal engagement point can be obtained
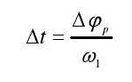
Where ω 1 is the angular velocity of the driving wheel.
The percentage of impact time in the whole meshing period can be obtained from the impact time Δ t obtained above
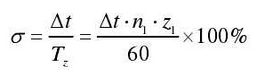
According to the above derived results, it can be seen that when the gear size parameters are determined, the meshing impact time Δ t is only related to the comprehensive deformation of the meshing teeth pair (other factors affect the impact time through δ). The load torque is an important factor affecting the comprehensive deformation δ. As shown in the figure, the impact time of the input stage teeth of an electric vehicle changes with the load.
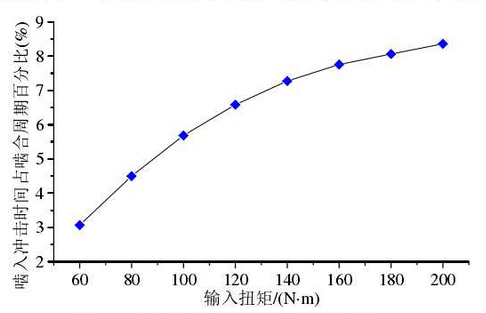
It can be seen from the figure that the percentage of the meshing impact time to the meshing period is between 3% and 8.4%; and with the increase of the load torque, the increase speed of the percentage of the meshing impact time in the meshing period slows down. This is because the increase of the load torque will increase the contact area of the tooth surface and enhance the bearing capacity of the tooth surface, resulting in the increase of the comprehensive deformation amount δ.
