Abstract: This paper focuses on the dynamic characteristics of spur gear pairs considering meshing impact. Firstly, the classification and mechanism of meshing impact are introduced. Then, the methods for calculating time-varying meshing stiffness, load distribution rate, impact time, and impact force are presented. Based on these, nonlinear dynamic models with and without considering meshing impact are established. Through numerical analysis and comparison of bifurcation diagrams, TLE diagrams, phase diagrams, Poincaré mapping diagrams, and dynamic force-time history diagrams, the effects of various parameters on the nonlinear dynamic characteristics of the system are studied. The research results provide a theoretical basis for understanding the meshing impact mechanism and improving the dynamic performance of spur gear transmissions.

1. Introduction
1.1 Research Background and Significance
Gear transmissions are widely used in mechanical systems and are crucial for high-speed, high-precision, heavy-load, and high-efficiency applications. However, meshing impact in gear transmissions can cause vibrations and noise, affecting the stability and reliability of the system. Therefore, studying the dynamic characteristics of spur gear pairs under meshing impact is of great significance for improving gear transmission performance.
1.2 Research Status at Home and Abroad
- Dynamic Modeling of Gear Transmission Systems: Scholars have developed various dynamic models, from non-time-varying to time-varying, and from single-stage to multi-stage transmissions. Modeling methods include the lumped mass method, finite element method, and concentrated parameter method. However, existing models often overlook the coupling effect of meshing impact and multi-state meshing characteristics.
- Nonlinear Dynamic Characteristics of Gear Transmission Systems: The nonlinear dynamic behavior of gear transmission systems is complex. Researchers use analytical, numerical, and experimental methods to study the dynamic characteristics and analyze the influence of parameters. However, the coupling effect of meshing impact and multi-state meshing on the dynamic characteristics needs further exploration.
- Meshing Impact Dynamic Characteristics of Gear Transmissions: Many studies have focused on the calculation and analysis of meshing impact forces and times. However, a more in-depth understanding of the meshing impact mechanism and its impact on the overall system is still required.
1.3 Research Objectives and Contents
- Research Objectives: This paper aims to investigate the meshing impact mechanism of spur gear pairs, establish corresponding dynamic models, and analyze the impact of system parameters on the dynamic characteristics to provide a theoretical basis for reducing vibration and noise.
- Research Contents: The paper includes the classification and calculation of meshing impact, the establishment and analysis of nonlinear dynamic models with and without considering meshing impact, and the study of the influence of various parameters on the system dynamics.
2. Spur Gear Pair Meshing Characteristics and Impact Mechanism
2.1 Meshing States of Spur Gear Pairs
The meshing process of spur gear pairs can be divided into single-tooth and double-tooth meshing regions. Due to the non-integer coincidence degree and the existence of backlash, there are five meshing states: double-tooth meshing on the driving side (MSdd), single-tooth meshing on the driving side (MSds), disengagement, double-tooth meshing on the back side (MSkd), and single-tooth meshing on the back side (MSks). The meshing states can be determined by the relationship between the dimensionless relative displacement and the backlash half-value D0.
2.2 Time-Varying Meshing Stiffness Calculation
The time-varying meshing stiffness is an important parameter in gear dynamic models. Using the potential energy method, the meshing stiffness can be calculated by considering the compression potential energy, shear potential energy, bending potential energy, Hertz contact potential energy, and matrix potential energy. The formula for calculating the time-varying meshing stiffness K(T) is as follows:
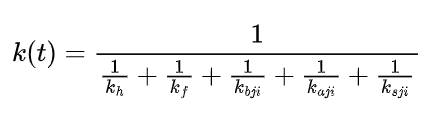
where Kh is the Hertz contact stiffness, Kf is the matrix stiffness, and Kbji, Kaji, and Ksji are the bending, axial compression, and shear stiffnesses of the meshing teeth, respectively.
2.3 Time-Varying Load Distribution Rate
The load distribution rate along the meshing line varies due to the non-integer coincidence degree of the gear. The formula for calculating the load distribution rate Ljc(t) is given by:
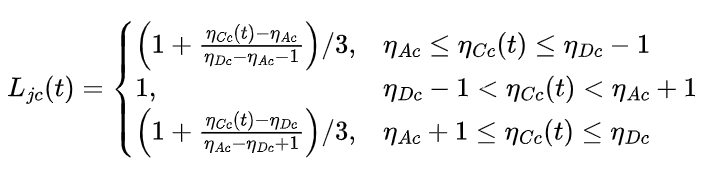
where ηic are the tooth profile parameters at different meshing positions.
2.4 Meshing Impact Mechanism Analysis
Meshing impact can be divided into two categories: tooth switching impact and boundary impact. Tooth switching impact includes single-to-double and double-to-single tooth switching impacts, which occur at the tooth switching points. Boundary impact occurs when the gear teeth transition from disengagement to meshing or backside contact. The impact force and time can be calculated based on the Hertz contact theory and the dynamic characteristics of the gear pair.
3. Nonlinear Dynamic Modeling Considering Tooth Switching Impact
3.1 Impact Time Calculation
The impact time is determined by the meshing stiffness and the relative initial velocity before impact. By simplifying the gear pair as two elastic bodies in contact, the impact process can be modeled using the Hertz contact theory. The compression time ts and the recovery time tγ can be calculated as follows:
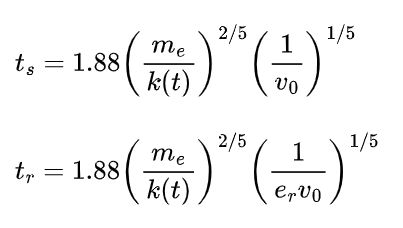
where me is the equivalent mass, v0 is the relative initial velocity, and er is the restitution coefficient.
3.2 Impact Force Calculation
The impact force varies during the impact process. In the compression stage, it increases sinusoidally, and in the recovery stage, it decreases cosinusoidally. The maximum impact force Fimax can be calculated using the formula:
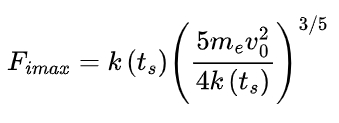
The impact force at any time during the impact can be expressed as:
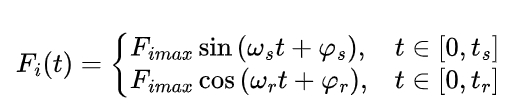
where ωs and ωr are the frequencies in the compression and recovery stages, and φs and φr are the initial phases.
3.3 Nonlinear Dynamic Model Establishment
Based on the multi-state meshing characteristics of the spur gear pair and the calculated impact time and force, a nonlinear dynamic model considering tooth switching impact is established. The dynamic equations for different meshing states, including tooth surface meshing and backside contact, are derived using Newton’s second law. The dimensionless normalized model is also obtained to facilitate numerical analysis.
3.4 Dynamic Characteristics Analysis
By using the Runge-Kutta method to solve the nonlinear dynamic equations, the dynamic characteristics of the gear pair under different parameters are analyzed. The results show that tooth switching impact affects the dynamic force and phase trajectory. The dynamic force changes from a jump to a gradual transition at the tooth switching position, and the phase trajectory becomes non-smooth. The effects of parameters such as meshing frequency, load, damping, and backlash on the system dynamics are also studied.
4. Nonlinear Dynamic Modeling Considering Meshing Impact
4.1 Boundary Impact Force Calculation
The boundary impact occurs at the boundaries of tooth surface meshing and backside contact. The critical normal forces after tooth surface and backside boundary impacts, [Fn]m and [Fn]c are calculated based on the gear meshing principle and energy conservation. The impact force at the end of the boundary impact can be determined using the formula:
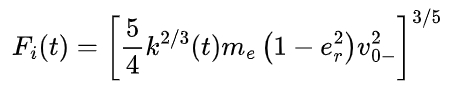
where v0- is the initial velocity before the boundary impact.
4.2 Dynamic Model Considering Meshing Impact
Based on the calculated boundary impact forces and the dynamic model considering tooth switching impact, a nonlinear dynamic model considering the overall meshing impact is established. The model takes into account the different motion states after boundary impact, such as tooth separation or continued meshing. The dimensionless nonlinear dynamic equations are derived to describe the system behavior.
4.3 Dynamic Characteristics Analysis
Using the established model, the dynamic characteristics of the gear pair under different operating conditions are analyzed. Five typical cases are considered to study the motion state transitions. The effects of parameters such as meshing frequency, load, damping, and comprehensive transmission error on the system dynamics are investigated. The results show that meshing impact has a significant impact on the system’s dynamic characteristics, including changes in motion states, phase trajectories, and dynamic forces.
5. Parameter Influence Analysis
5.1 Influence of Meshing Frequency
The meshing frequency directly affects the transmission speed of the gear pair. As the meshing frequency increases, the system’s dynamic behavior becomes more complex. In the low-frequency range, the impact of meshing impact on the system is relatively small. However, in the high-frequency range, especially when the meshing frequency is within the multiple frequency range, the system may exhibit chaotic motion. The dynamic characteristics of the system, such as the motion state, phase trajectory, and dynamic force, change significantly with the meshing frequency.
5.2 Influence of Load
Load is an important parameter that reflects the power transmission level. When the load is small, the gear pair may experience complex motion, including tooth back contact and boundary impact. As the load increases, the system tends to be more stable, and the impact of meshing impact decreases. The load also affects the dynamic force and motion state of the gear pair. A reasonable load range can ensure the stable operation of the gear transmission.
5.3 Influence of Damping
Damping reflects the friction coefficient between the gear teeth. Increasing the damping can reduce the vibration of the system. When the damping coefficient is small, the system may exhibit chaotic motion. By selecting an appropriate damping value, the stability of the system can be improved. The damping also affects the dynamic force and motion state of the gear pair, and different damping coefficients result in different dynamic responses.
5.4 Influence of Comprehensive Transmission Error
The comprehensive transmission error is an internal excitation error in the gear transmission system. A small error has a negligible impact on the system. However, as the error increases, the meshing state of the gear pair becomes more complex, and the system may exhibit chaotic motion. The comprehensive transmission error also affects the dynamic force and motion state of the gear pair, and different error values lead to different dynamic characteristics.
6. Conclusion and Outlook
6.1 Research Conclusions
- The meshing impact of spur gear pairs is classified into tooth switching impact and boundary impact. Considering these impacts, the dynamic model is more consistent with the actual operation of the gear.
- The dynamic force at the tooth switching position changes from a jump to a gradual transition after considering tooth switching impact. The boundary impact causes a jump in the relative velocity amplitude at the meshing and backside contact boundaries.
- Different system parameters have different effects on the dynamic characteristics of the gear pair. Reasonable parameter selection can improve the stability and reduce the vibration of the system.
6.2 Research Innovations
- A method for identifying the meshing impact type of spur gear pairs is proposed, providing a basis for analyzing the meshing impact characteristics.
- A nonlinear dynamic model considering meshing impact is established, which can be used for further research on gear transmission systems.
