In ADAMS simulation software, for any mechanical system with motion constraints, the first Lagrange equation with Lagrange multiplier is used to represent the motion of the system in the form of energy

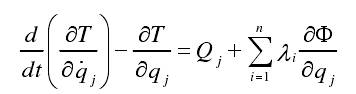
Where:

T — represents the kinetic energy of the system;

QJ represents the velocity in the generalized coordinate system;

J — the direction of coordinates;

QJ — represents generalized coordinates;

QJ — generalized force in generalized coordinate direction;

θ — constraint equation of system dynamics;

λ I — denotes Lagrange multiplier.

The generalized coordinate vector of the position and orientation of the rigid body is as follows:

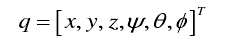
Define the direction coordinates of movement and rotation as follows:

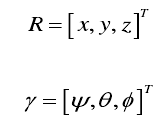
The kinetic energy of the system is expressed as follows:

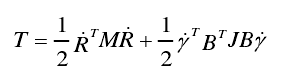
Where:

R — velocity of rigid body moving direction;

M — mass matrix of component;

γ – velocity of rigid body in rotation direction;

B — transformation matrix from generalized coordinate system to centroid coordinate system;

J — moment of inertia matrix of component in centroid coordinate system.

The generalized momentum is introduced

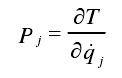
After simplification, the reaction force of the constraint is as follows:

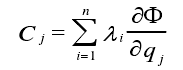
The dynamic equations of the system are obtained as follows:

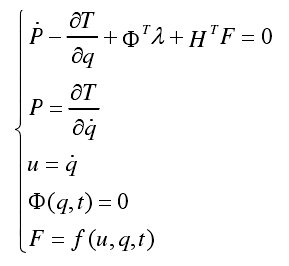
Where:

H — represents the load coordinate transformation matrix;

F — vector representing load.