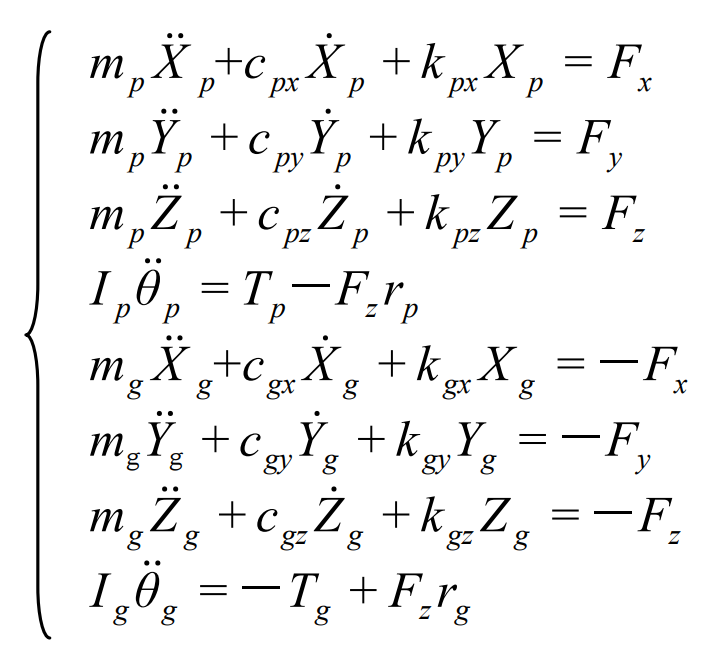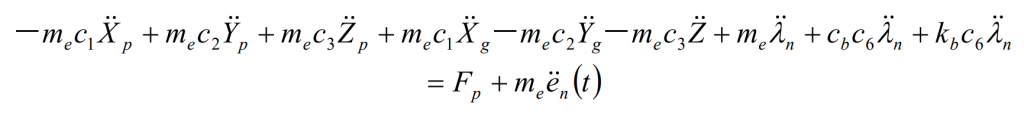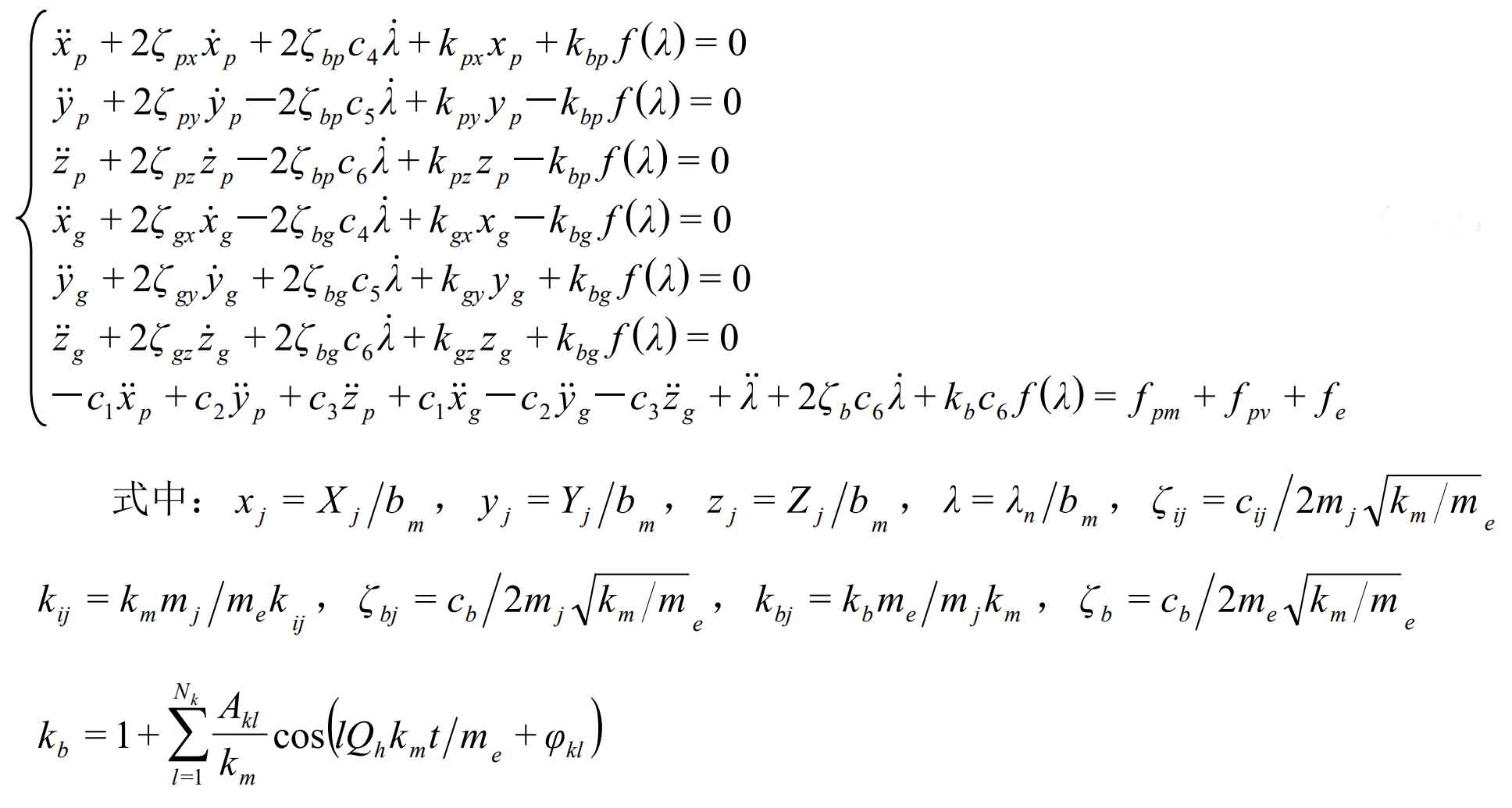According to Newton’s second law and the balance condition of force, the dynamic equation of the straight bevel gear transmission model shown in the figure is:
Where MP and Mg are the masses of the two straight bevel gears respectively, and IP and Ig are the moment of inertia of the two straight bevel gears respectively. From the dynamic geometric model of straight bevel gear, it can be seen that the torsional displacement of driving wheel 1 around X axis is θ p. The torsional displacement of the driven wheel 2 around the y-axis is θ g. The relative displacement n of the normal of the meshing point λ The expression is substituted into the dynamic equation of straight bevel gear to eliminate the torsional displacement θ p, θ g. After combined calculation, the following formula is obtained:
Where, me is the equivalent mass of straight bevel gear pair; FP is the circumferential force of the driving straight bevel gear.
Because the order of magnitude of each physical quantity in the straight bevel gear dynamic equation is inconsistent and varies greatly, it will bring great difficulties to the numerical calculation and solving the equation. Therefore, the above straight bevel gear dynamic equation must be dimensionless before solving the equation.
By dimensionless treatment of the above dynamic equation of straight bevel gear, the quantified equation can be obtained as follows: