In the established five-gear manual transmission model, there is coupling of finite element model, and the number of degrees of freedom of finite element model is huge. In order to improve the calculation ability, component mode synthesis (CMS) proposed by Craig and Bampton is used for dynamic reduction.The greatest advantage of this method is that it can greatly reduce the data of finite element models, which is dependent on the frequency range concerned and independent of the degree of freedom. In addition, if a component is consistent at different mode frequencies, only one solution is required.Unlike the Guyan method, the CMS method incorporates both mass and speed.

For components without damping, the equation of motion is:

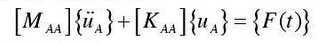
Craig-Bampton transformation (cb) is defined as dividing the degrees of freedom of a flexible finite element model into boundary degrees of freedom UB (also called connection degrees of freedom) and internal degrees of freedom uL, which are preserved intact without mode transformation.That is to say,

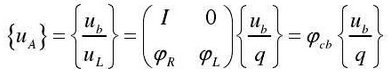
By combining the two formulas, one can obtain:

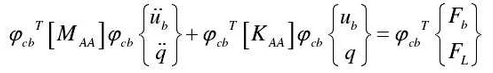
Define the mass and stiffness matrix:

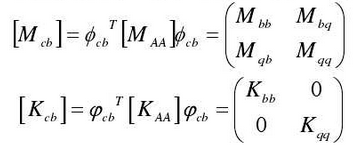
Finally, the dynamic motion equation considering damping is written by using C-B transformation:

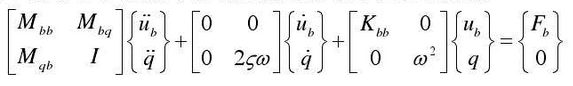
The reduction process is carried out when super-elements are formed in finite element analysis. The external joint retained when establishing the flexible super-element model is the connection point when merging into the multi-body model. Its degree of freedom is the degree of boundary freedom in the CMS method. Through the connection point, various boundary conditions can be established in the multi-body model.When a super-unit is converted into a multi-body model, the flexible body is written as a modal neutral file (MNF). At this point, the orthogonal mode transformation is performed to remove the rigid body mode and retain all the information of the flexible body mode.