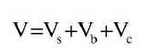From the analysis results, it can be seen that the influence of the degree of freedom of swing is relatively small in the range of engine operating speed. Therefore, the influence of the degree of freedom of swing is neglected while ensuring the calculation accuracy and considering the calculation efficiency.The centralized mass method is used to simplify the gear drive system of the tracked vehicle shown in the figure.
The engine internals and the active end of the coupling are simplified to a centralized mass point, while the passive end of the coupling, the front drive and the input connecting disc are simplified to a centralized mass point.Except that there is only one degree of torsional freedom at the centralized mass point composed of the engine internals and the active end of the coupling, there are two degrees of lateral translation freedom and one degree of torsional freedom at the other centralized mass points.The simplified centralized parameter model of the gear drive system for tracked vehicles shows 43 centralized mass points and 127 degrees of freedom.
Lagrange method is used to establish the non-linear dynamic models of transverse-torsional coupling of each retainer.The kinetic energy function of the gear drive system of tracked vehicle can be obtained by summing the kinetic energy functions of each concentrated mass point.
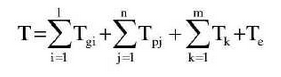
I n the formula, Tg and Tp are the kinetic functions of fixed-axle gear drive and planetary gear drive respectively; Te is the kinetic energy function of the centralized mass point composed of the internal components of the engine and the active end of the coupling; Tk is the kinetic energy function of the centralized mass points such as the remaining bearings, clutches and inertia discs; I is the number of fixed-axle gear drives, I=5; n is the number of planetary gear drives, n=2; m is the bearing, clutch, etc.Total number of mass points, m=18, equal to the inertia disc and the actuator.The kinetic functions of fixed-shaft gear drive and planetary gear drive need to be neglected at the same time.The kinetic energy functions of the remaining concentrated mass points, such as bearings, clutches and inertia discs, can be expressed as:
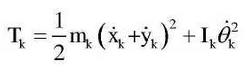
The potential energy function of the gear drive system mainly includes the potential energy caused by the deformation of components such as drive shaft, bearing, clutch and connecting piece, among which the potential energy function caused by the vibration displacement of each concentrated mass point on the drive shaft is:
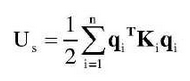
The rolling bearing is simplified as an isotropic elastic support with the elastic potential energy due to the bearing deformation:
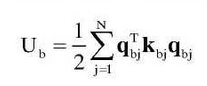
The active and passive edge and planetary drive connection components of the clutch are equivalent to spring and damper connections at their respective degrees of freedom. The potential function due to relative deformation of the mass points connected is:
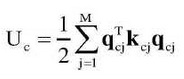
By summing up the formulas, the potential energy function of the gear drive system is:
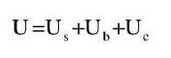
The energy dissipation function of the system is similar to that of the potential function. By changing the stiffness coefficient of the potential function into damping coefficient and replacing the displacement in the potential function with velocity, the potential energy function of the gear transmission system is obtained as follows: