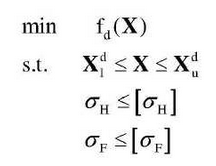Based on the dynamic and static characteristics, the optimization model of tooth profile modification is established, and the optimization design of multiple modification parameters is carried out, and then the optimization results are compared and analyzed. In the following, taking dynamic characteristics as the optimization objective is called dynamic performance optimization model, and taking static characteristics as the optimization objective is called static performance optimization model. The optimization model includes three elements: design variables, objective functions and constraints, which are different according to different design requirements.

(1) Design variables

Take the maximum modification amount cmax1 and cmax2 and the modification length L1 and L2 of each gear top position in the gear pair as the design variables, as shown in the figure. The two gears adopt the same modification type, and the coefficient a related to the modification type in the formula is taken as the design variable. Therefore, the optimization model consists of five independent design variables:

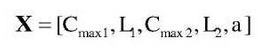
(2) Objective function

The vibration of gear transmission system is generally evaluated by dynamic load, and the dynamic load coefficient defined by the formula is taken as the dynamic performance optimization objective:

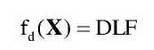
(3) Constraints

Constraints include boundary constraints and performance constraints, where boundary constraints are the boundary conditions of design variables:

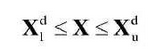
Among them, the upper limit of the optimal modification amount is 0.022mm of the comprehensive deformation of the highest point of single tooth engagement under the action of the average torque of the engine, the upper limit of the modification length is 7mm of the corresponding modification length of the highest point of single tooth engagement, and the boundary condition of the correlation coefficient with the modification type is 0 less than or equal to a less than or equal to 1.

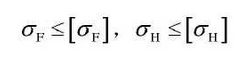
Performance constraints include gear bending fatigue strength and contact fatigue strength constraints.

The non-linear dynamic model of the gear transmission system considers the external engine excitation, and the dynamic load coefficient is determined by the formula, so it can replace the use coefficient and dynamic load coefficient in the formula of checking the bending fatigue and contact fatigue strength of the gear.