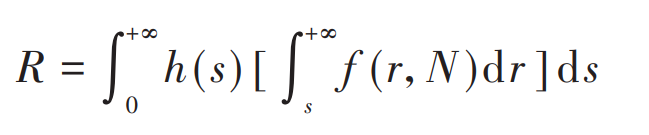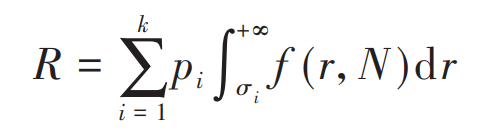Variation law of residual strength of planetary gears in flight vehicle transmission system. Taking the bending fatigue residual strength of each gear in the planetary gear train as an example, the initial static fatigue strength R (0) follows the normal distribution of n (500, 50). The degradation law of its average strength is shown in the figure. In this model, it is considered that in the process of strength degradation, the distribution type and standard deviation remain unchanged, and only the mean value of strength changes.
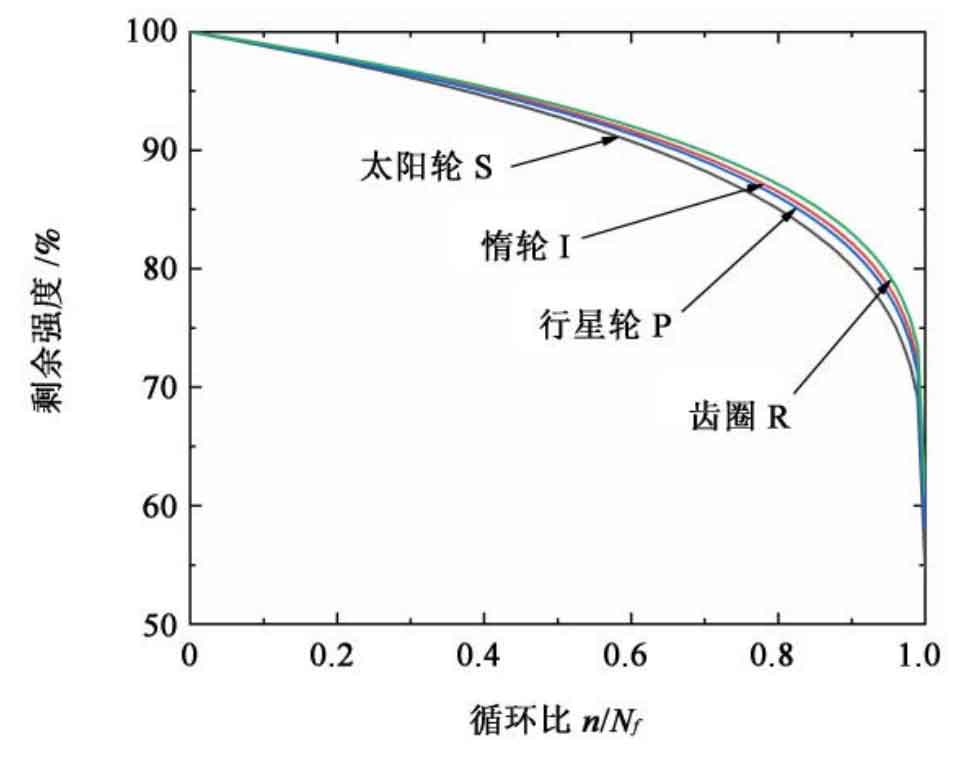
Thus, the variation law between the strength degradation of planetary gears and the number of cycles can be obtained. The strength degradation of planetary gears is relatively gentle in the early and middle stages, while it degrades sharply in the final stage, which is in line with the “sudden death” characteristics of metal materials.
When the number of cycles is n and the probability density function of fatigue strength is f (R, n), the reliability calculated by stress strength interference theory is:
Where H (s) is the probability density function of stress variable s. Based on the established load spectrum, the planetary gears are subjected to multistage loads. Therefore, the stress strength model can be extended to take the probability PI (I = 1, 2,…, K, Σ Pi = 1) take K (k = 1, 2,…, 5) stress levels σ The case of symmetrical cyclic load of I, i.e.:
Where, the occurrence probability Pi of each stress level is the proportion of its mission profile time to the total flight time.