Abstract
This study investigates the dynamic reliability of a wind turbine gearbox under random wind loads, focusing on failure correlation between components. A 2MW gearbox system is modeled using a gear-shaft-bearing dynamic framework, incorporating time-varying meshing stiffness and composite errors. The dynamic meshing forces under constant loads are derived, while a Weibull-distributed stochastic wind model generates external excitations. Stress-time histories under variable loads are obtained by combining internal dynamic forces and external wind-induced torques. Gamma processes simulate material strength degradation based on P-S-N curves, and a hybrid Copula model addresses failure dependencies at both component and system levels. Results highlight that contact fatigue dominates early service stages, while bending fatigue becomes critical in later phases. System reliability analysis considering failure correlation yields more realistic predictions than independence assumptions.
1. Introduction
Wind turbine gearboxes are critical for power transmission but face reliability challenges due to stochastic loads and component interactions. Traditional reliability models often ignore failure dependencies, leading to conservative or unrealistic predictions. This work integrates dynamic modeling, stochastic wind loads, strength degradation, and hybrid Copula functions to evaluate gearbox reliability.
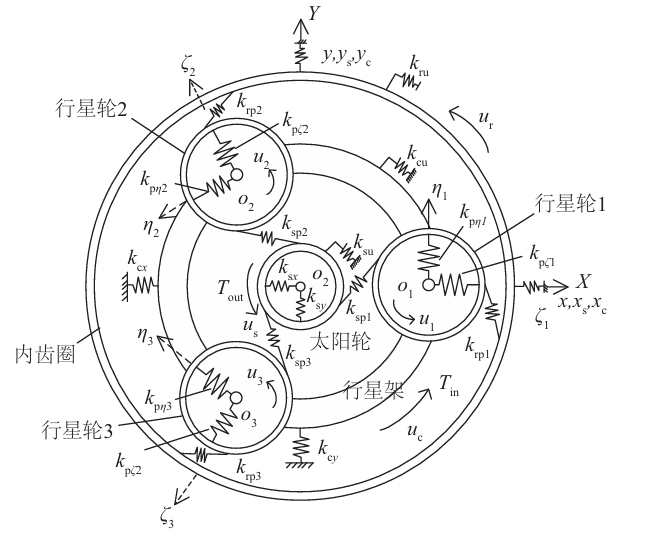
2. Dynamic Modeling of Gearbox Transmission System
2.1 Gear-Shaft-Bearing Dynamic Model
The gearbox comprises a planetary stage and two parallel-axis stages. The dynamic equations for the planetary gear train are expressed as:Mq¨+[Kb(t)+Km(t)+Ku(t)]q=T(t)
where:
- M: Mass matrix
- Kb, Km, Ku: Bearing, meshing, and torsional stiffness matrices
- q: Displacement vector
For parallel-axis gears, the finite element model includes 32 nodes with translational and rotational DOFs.
2.2 Key Geometric Parameters
Table 1 summarizes gear parameters.
Table 1. Geometric Parameters of Gearbox Components
| Gear | Teeth (z) | Module (m, mm) | Pressure Angle (α, °) | Face Width (b, mm) |
|---|---|---|---|---|
| Sun | 21 | 17 | 20 | 370 |
| Planet | 38 | 17 | 20 | 370 |
| Ring | 99 | 17 | 20 | 370 |
| G1 | 92 | 16 | 20 | 300 |
| G2 | 21 | 16 | 20 | 300 |
3. Stochastic Wind Load and Stress Analysis
3.1 Weibull Wind Speed Model
Wind speed v follows a Weibull distribution:fw(v)=ck(cv)k−1exp[−(cv)k]
Parameters k=4.9 and c=8.7m/s are derived from wind field data.
3.2 Torque Calculation
Input torque T varies with wind speed:T=⎩⎨⎧0,vrate2Tratev2,Trate,0,v<vcut-invcut-in≤v<vratevrate≤v<vcut-offv≥vcut-off
3.3 Stress-Time History
Dynamic contact stress σH and bending stress σF are calculated as:σH=ZEZHZβZεdbKAKVKHβKHαFt⋅uu+1σF=bmKAKVKFβKFαFtYFaYSaYεYβ
4. Dynamic Reliability Modeling
4.1 Strength Degradation via Gamma Process
Component strength σ(t) degrades as:G(d∣ν(t),μ)=Γ(ν(t))μν(t)dν(t)−1e−μd
Parameters ν(t) and μ are derived from P-S-N curves (Table 2).
Table 2. Strength Degradation Parameters for 20CrMnTi Steel
| Survival Rate (P) | me | C |
|---|---|---|
| 0.99 | 28.5714 | 1.08×10102 |
| 0.95 | 21.8866 | 7.10×1079 |
4.2 Hybrid Copula Model for Failure Correlation
Joint failure probabilities are modeled using Gumbel, Clayton, and Frank Copulas:CG(u,v;θ)=exp[−((−lnu)θ+(−lnv)θ)1/θ]CC(u,v;α)=(u−α+v−α−1)−1/αCF(u,v;γ)=−γ1ln[1+e−γ−1(e−γu−1)(e−γv−1)]
A weighted hybrid Copula combines these functions:Chybrid=εGCG+εCCC+εFCF
5. Case Study and Results
5.1 Input Parameters
A 2MW gearbox with vcut-in=3.5m/s, vcut-off=25m/s, and vrate=17r/min is analyzed.
5.2 Stress Distribution and Reliability Trends
- Contact stress dominates early failures (e.g., sun gear reliability drops to 0.98 after 1.5 years).
- Bending fatigue governs later stages (e.g., parallel-axis gear G4 reaches critical reliability at 6 years).
Table 3. Reliability Thresholds for Critical Gears
| Gear | Contact Fatigue (Years) | Bending Fatigue (Years) |
|---|---|---|
| Sun | 1.5 | >10 |
| G4 | 6.0 | 8.0 |
5.3 System Reliability Comparison
- Independent assumption: Rsystem=0.1396 at 20 years.
- Copula-based model: Rsystem=0.2975 at 20 years.
6. Conclusions
- Contact Fatigue: Critical in early gearbox service; maintenance should prioritize gear inspections.
- Bending Fatigue: Dominates later stages; parallel-axis gears (e.g., G4) require focused monitoring.
- Failure Correlation: Hybrid Copula models improve accuracy, showing 113% higher reliability than independence assumptions.
- Dynamic Modeling: Integrating stochastic loads and strength degradation enables realistic lifetime predictions.
This work provides a framework for optimizing wind turbine gearbox design and maintenance strategies, ensuring enhanced reliability under real-world operating conditions.
