The original 20 node finite element method is adopted, which takes the eight vertices and the midpoint of twelve edges of hexahedron as the nodes. However, due to the difference of the shape function between the eight vertices of hexahedron and the midpoint of twelve edges, the flexibility value of the edge midpoint is distorted when calculating the flexibility value of the tooth surface node by the flexibility matrix method, so the 8-node isoparametric finite element method is adopted. This isoparametric element satisfies the irregular geometry of spiral bevel gear. Using this element, we can better approach the boundary of spatial structure. 8-node finite element takes eight vertices of hexahedron as nodes as shown in Figure 1, numbered I1, I2, I3,… I8. The overall coordinates of these 8 nodes are (x1, Y1, z1), (X2, Y2, Z2)… (x8, Y8, Z8). Then set up local parameter coordinates for the 8 nodes of the unit, which are( ξ 1, η 1, ζ 1),( ξ 2, η 2, ζ 2),( ξ 3, η 3, ζ 3),…,( ξ 8, η 8, ζ 8) The interpolation displacement function of the eight node hexahedral element is:
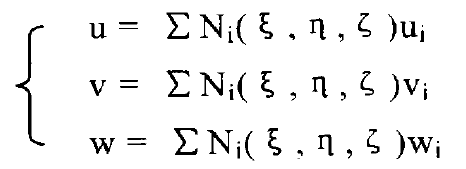
The coordinate transformation formula of the eight node hexahedral element is:
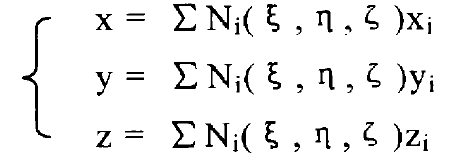
The geometric equation of three-dimensional space problem is:
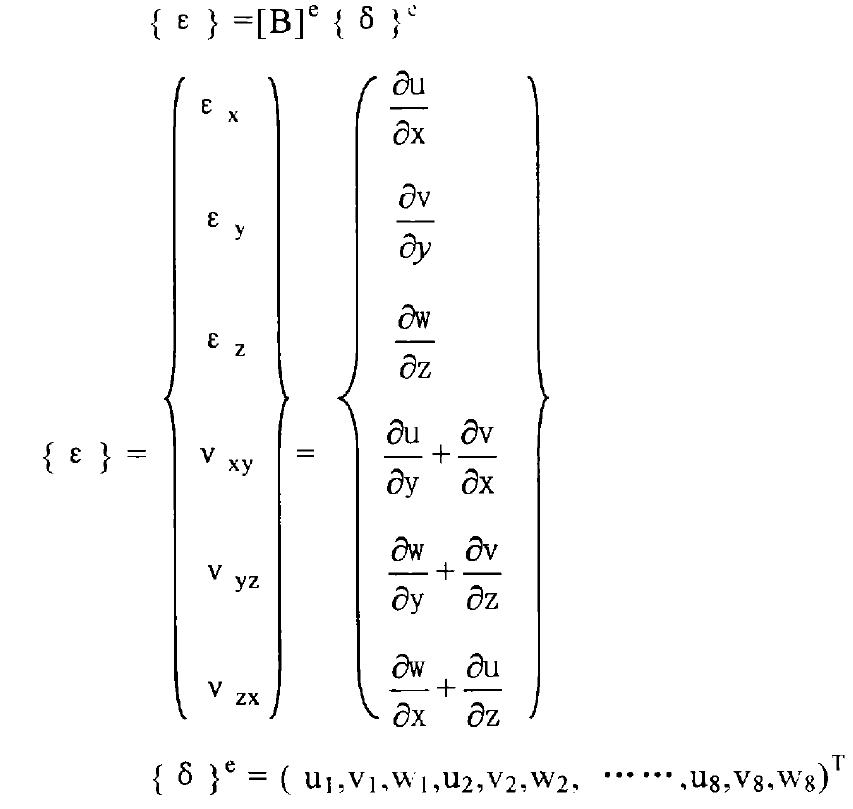
{ δ} E represents the node displacement value of the element, and the geometric matrix [b] e is:

Of which:
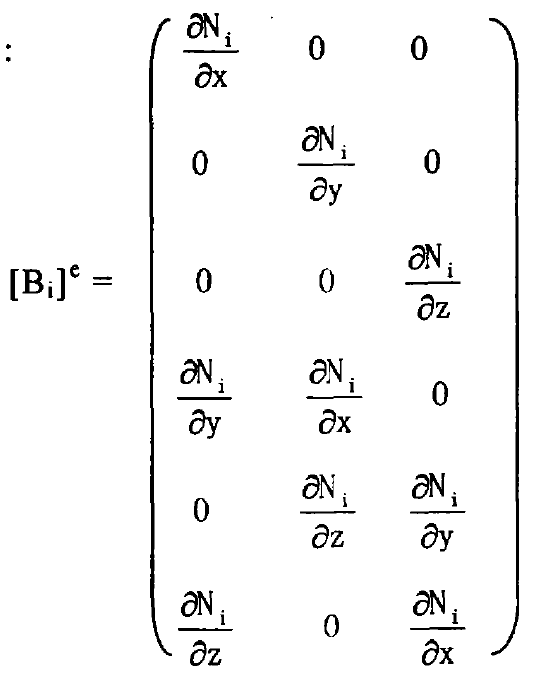
Subscript i = 1,2,…, 8 in [Bi] E.
The stiffness matrix of 8-node hexahedral element is:
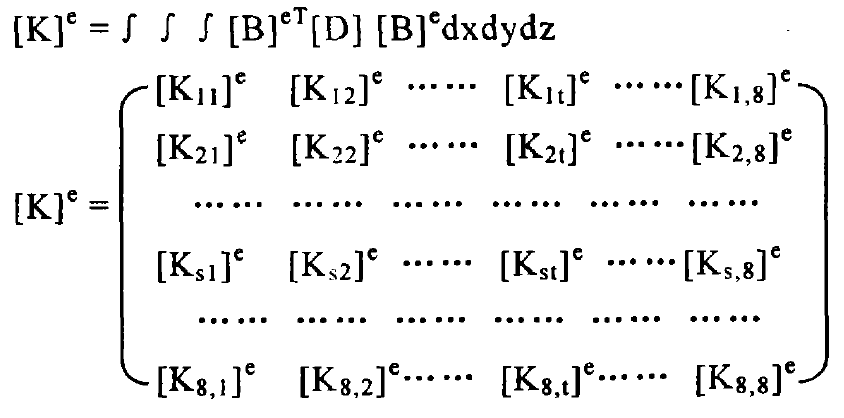
The sub matrix [KST] e of the stiffness matrix [k] e of the 8-node hexahedral element is:
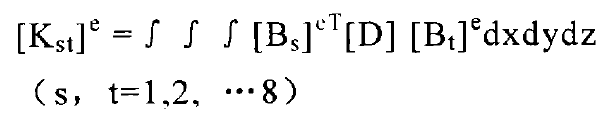
The shape function Ni (I = 1,2,…, 8) is a function of local coordinates. Therefore, it is explained by the formula that the overall coordinates (x, y, z) are local coordinates( ξ,η,ζ) That is, the transformation between global coordinates and local coordinates. The derivation rules according to the composite function are:
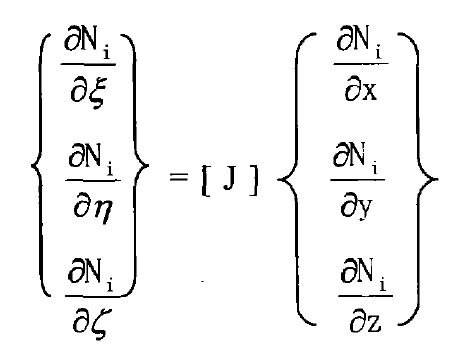
In the above formula, [J] represents the relationship between global coordinates and local coordinates.

Find the inverse matrix [J] – 1 of Jacobian matrix [J], which can be obtained by formula Transformation:
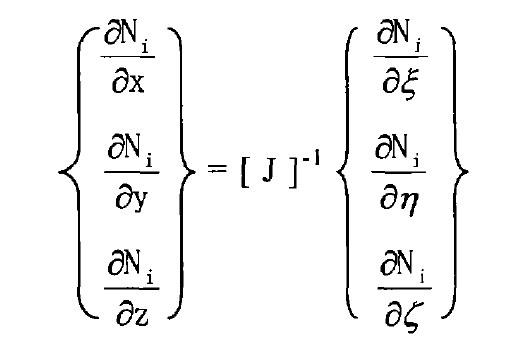
For the nine three-dimensional integrals in the formula, the numerical integration method can also be used, that is, appropriately select some integration points in the hexahedron, calculate the values of the integrand function at these integration and points, and then calculate the values of the integration formula according to these values. Gauss quadrature formula can be used to obtain higher precision integral value with fewer integration points, and the formula can be transformed into:
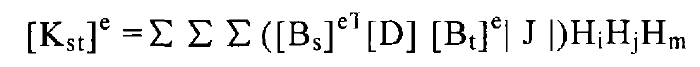
Where Hi, HJ and HM are weighting coefficients. The stiffness matrix of the element is obtained, and then all of the whole structure are calculated as above. Then, the method of forming the structural stiffness matrix according to the element or the structural stiffness matrix according to the node is combined. Finally, the overall structural stiffness matrix [k] can be obtained.
For spatial problems, the stress state of a point consists of six stress components, namely:
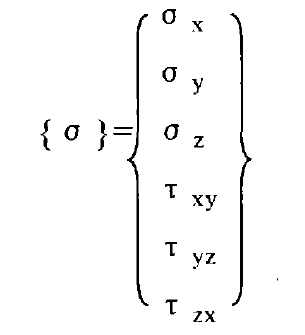
Therefore, the stress-strain equation representing the physical relationship between stress component and strain in spatial problem is:
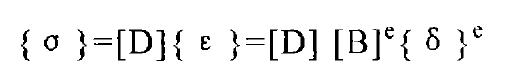
Of which:
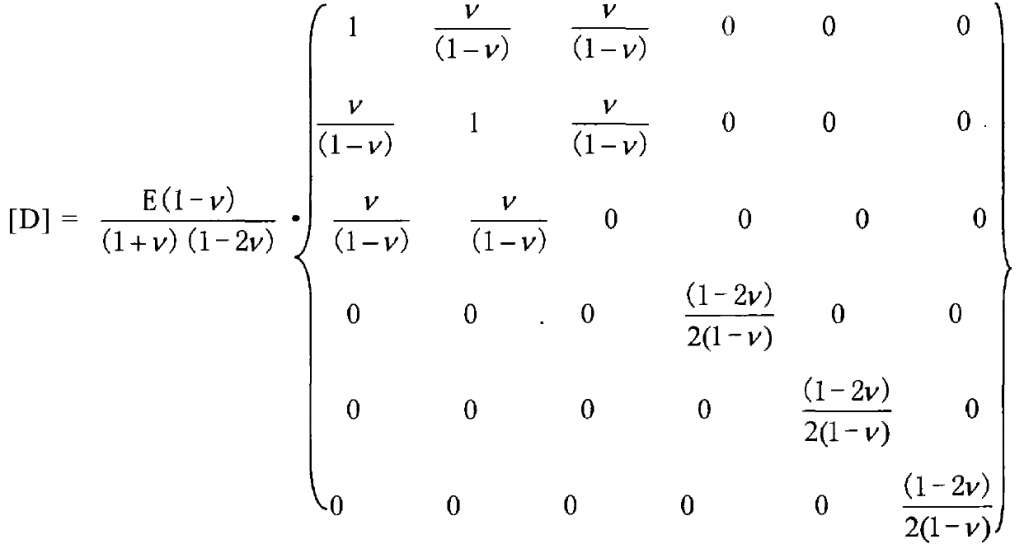
Where:
E – elastic modulus of material
V – Poisson’s ratio of material

